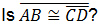Select the counter example for the statement:

If two rays have the same endpoint, then they are opposite rays.

1. 
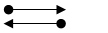
   Incorrect. The two rays do not have the same endpoint.
2. 
   Incorrect. This supports the conditional statement, it is not a counter example.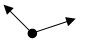
3. 
   Correct! The rays share a common endpoint but they form an angle and not opposite rays, therefore it is an accurate counter example.
4. 
   Incorrect. The line segment doesn’t have any relevance to the conditional statement.

Select the mathematical statement with a truth value.

1. An Isosceles Triangle has two congruent sides.
   Correct! This mathematical statement has a truth value that can be evaluated.
2. Angle A is an obtuse angle.
   Incorrect. Since the measure of angle A is not given the truth value cannot be determined.
3. 
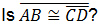
   Incorrect. This is a question and questions are not mathematical statements.
4. x + 2y = 22
   Incorrect. This statement contains unknown variables that cannot be evaluated for a truth value.

Select the conditional statement that is the correct interpretation of the Venn diagram.

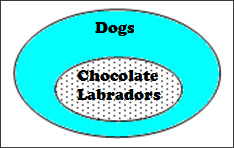
A. All dogs are Chocolate Labradors.
Incorrect. This is the converse of the conditional statement.

B. All Chocolate Labradors are dogs.
Correct! This is a conditional statement.

C. All dogs are not Chocolate Labradors.
Incorrect. This is a negation.

D. Are all Chocolate Labradors dogs?
Incorrect. This is a question.

Select the statement that has the same truth value as its converse.

1. If an angle measures 90°, then it is an obtuse angle.
   Correct! The converse is “If the angle is an obtuse angle, then the angle measures 90° which is false and so is the original conditional statement.
2. If an angle measures 147°, then it is an obtuse angle.
   Incorrect. The converse is “If the angle is an obtuse angle, then the angle measures 147° which is false because an obtuse angle can be any measure greater than 90° and less than 180°; the original conditional statement was true.
3. If it is a linear pair of angles, then the angles are supplementary.
   Incorrect. The converse is “If the angles are supplementary, then they are a linear pair,” this is false because not all supplementary angles have to be a linear pair; and the original conditional statement was true.
4. If two angles are acute angles, then they are complementary.
   Incorrect. The converse is “If two angles are complementary, then they are acute angles” which is true and the original statement was false because two acute angles are not always complementary.

Determine the truth value of the converse of the following statement and, if it is false, find the correct counter example:

If a figure is a rectangle, then it is a quadrilateral.

A. If a figure is a rectangle, then it is a quadrilateral: True
Incorrect. This is true but it restates the original conditional statement.

B. If a figure is a quadrilateral, then it is a polygon: True
Incorrect. This is true but it isn’t the converse of the original conditional statement.

C. If a figure is a quadrilateral, then it is a rectangle: False, the counter example: a rhombus is a quadrilateral but not a rectangle.
Correct! This is the converse statement and it is false because every quadrilateral is not a rectangle.

D. If a figure is a quadrilateral, then it is not a rectangle: False, the counter example: a rectangle could be a quadrilateral.
Incorrect. This is not the converse of the original conditional statement.