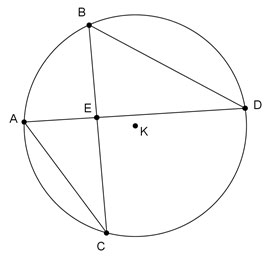
Given: Circle K with m∠ACB = 25° and Point E is the intersection of AD and BC.

What can you conclude from this diagram and given information?

A. ≅
Incorrect. We are not given information about angles with a vertex at Point E.

B. AC // BD
Incorrect. We do not know enough to make conclusions about angle relationships that would support parallel lines inside the circle.

C. ΔBED is isosceles, so ∠B ≅ ∠D, since the base angles of isosceles triangles are congruent.
Incorrect. Since Point E is not the center of the circle, BE and DE are not radii of circle K.

D. ∠ACB ≅ ∠ADB
Correct! If two angles inscribe the same arc, then they are congruent.

Given: Circle K is shown below with parallel chords AD and BC.

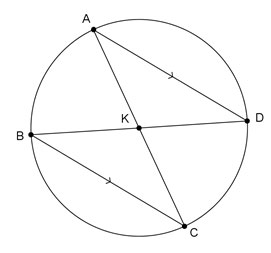
What can you conclude from this diagram and given information?

A. ≅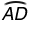
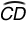
Incorrect. While this may appear to be true from the diagram, we do not know that two parallel chords create congruent arcs in the exterior region of the chords.

B. ≅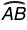
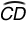
Correct! If two chords are parallel, then they create congruent arcs on a circle.

C. ∠ACB ≅ ∠AKB
Incorrect. These two angles intercept the same arc, and one is an inscribed angle while the other is a central angle. They cannot be congruent angles.

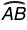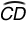D. m + m = 180°
Incorrect. A semicircle has an arc measure of 180°, but these two arcs may or may not create a semicircle when joined.

Circle Q is shown below with parallel chords AB and CE.

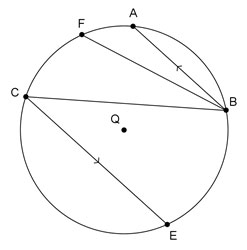
Which of the following statements is not always true?

A. ≅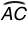
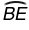
Incorrect. If two chords are parallel, then they intercept congruent arcs on the circle.

B. m∠ABC = m∠BCE
Incorrect. BC is a transversal that crosses parallel segments AB and CE, so alternate interior angles are congruent, and congruent angles have equal measures.

C. m∠ABF + m∠FBC = m∠ABC
Incorrect. The angle addition postulate shows that the sum of the measures of two adjacent, non-overlapping angles will equal the measure of the angle created by the two outside rays.

D. AB ≅ CE
Correct! The two chords will only be congruent if they are the same distance from the center, Point Q, and we do not know if that is the case in this figure.

A community college has a circular garden with three parallel sidewalks that pass through the garden, as shown in the diagram below. Each sidewalk has endpoints represented by a point on circle M, and sidewalk AB and sidewalk CE are the same distance from sidewalk FD.

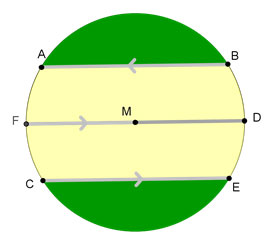
Based on the information shown in the diagram, which of the following statements must be true?

A. The length of 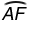is the same as the length of .
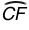Correct! Because parallel chords AB and CE are equidistant from diameter FD, they intercept arcs that are the same length with respect to the diameter.

B. CE > FD
Incorrect. Because FD is a diameter, it must be the longest chord in the circle.

C. MD > MB
Incorrect. Both MD and MB are radii of circle M, and all radii of a circle are congruent.

D. The length of 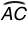is the same as the length of .
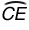Incorrect. There is not enough information in the figure to conclude a relationship between the lengths of these two arcs.

Circle Q is shown below with parallel chords AB and CE.

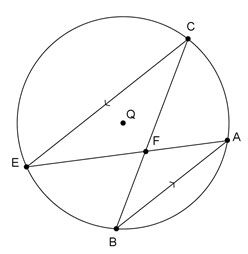
Which of the following statements may not always be true?

A. ∠EFC ≅ ∠AFB
Incorrect. These two angles are vertical angles, and vertical angles are always congruent.

B. ≅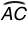
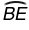
Incorrect. These two arcs are intercepted by parallel chords, and will always be congruent.

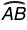C. m < m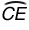
Correct! While this statement appears to be true in this figure, it will only be true if 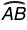is farther from the center of the circle than .

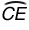D. ∠ECB ≅∠ EAB
Incorrect. These two angles are inscribed angles that intercept the same arc, and will always be congruent.