1. AD is longer than DC.
   Incorrect. Since D is the midpoint of AC, one segment is not longer than the other.
2. AD is congruent to AD.
   Incorrect. A line has infinite length, so it cannot be congruent to a segment.
3. AD is congruent to DC.
   Correct! A midpoint falls in the middle of the segment and forms two congruent parts.
4. AD is congruent to AC.
   Incorrect. AD is the length of the entire segment and AC only contains half of the original segment.

If points A, B and C determine plane D, which of the following conjectures best explains the relationship among points A, B, and C?

1. A, B, and C are collinear because they are in plane D.
   Incorrect. A, B, and C are noncollinear because of the postulate that states through any three noncollinear points there is exactly one plane containing them.
2. A, B, and C intersect plane D as a line and therefore are collinear.
   Incorrect. A, B, and C are noncollinear because of the postulate that states through any three noncollinear points there is exactly one plane containing them.
3. A, B, and C are noncollinear because they intersect plane D as a line.
   Incorrect. “Noncollinear” means that three points are not in a line.
4. A, B, and C are noncollinear because a plane is determined by 3 noncollinear points.
   Correct! This is the postulate defining a plane.

What is the greatest number of intersection points four coplanar lines can have?

A. 4
Incorrect. Look at a picture to test your conjecture.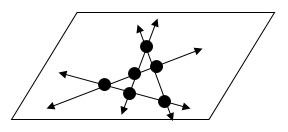

B. 6
Correct! Four non-coincident lines can intersect in at most 6 places.

C. 2
Incorrect. Look at a picture to test your conjecture.

D. 0
Incorrect. Look at a picture to test your conjecture.

In the figure, AD is 24 feet. What is AB in terms of x?

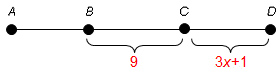
1. 14 3
   Incorrect. Remember the total segment length is 24, so AB is equal to 24 – (9 + 3x + 1).
2. 13 − 3x
   Incorrect. Remember the total segment length is 24, so AB is equal to 24 – (9 + 3x + 1).
3. 3x + 1
   Incorrect. Remember the total segment length is 24, so AB is equal to 24 – (9 + 3x + 1).
4. 14 − 3x
   Correct! You successfully subtracted the lengths of BC and CD then simplified the expression.

Points A, B, C, and D lie on the same line, in order, and AB ≅ CD, as shown in the figure below.

Is it true that AC ≅ BD? Explain.

1. Yes. AC ≅ BD because they each contain BC and one of two other congruent segments.
   Correct! Great job.
2. There is not enough information to conclude a relationship between AC and BD.
   Incorrect. What segment is contained in the overlap between AC and BD?
3. No. AC < BD, since A and C lie farther to the left on the line, and numbers on the left end of a number line are less than numbers on the right end.
   Incorrect. The points lie on a line, but this isn’t necessarily a number line.
4. No. AC ≠ BD. AB ≅ CD but BD does not equal CD, so AC = BD cannot be true.
   Incorrect. It is true that BD ≠ CD, but that does not necessarily mean that AC ≠ BD.