Using the polygons shown below, what can you conclude about the sum of the interior angles of any polygon?

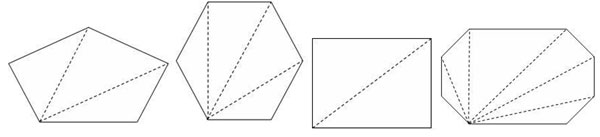
A. The sum of the interior angles is always 180 degrees.
Incorrect. To find the sum of the interior angles, multiply the number of triangles by 180.

B. The sum of the interior angles in a polygon is always 360 degrees.
Incorrect. The sum of the exterior angles of any polygon is 360 degrees. To find the sum of the interior angles, multiply the number of triangles by 180.

C. The sum of the interior angles in any polygon can be found by multiplying the number of triangles formed by the diagonals from one vertex times 180 degrees in each triangle.
Correct! The sum of the angles in each triangle is 180 degrees. Multiplying the number of triangles by 180 should give you the sum of the exterior angles in any polygon.

D. The sum of the interior angles in a polygon can be found by multiplying the number of sides times 180 degrees.
Incorrect. The number of triangles formed by the diagonals from one vertex is always 2 less than the number of sides. To find the sum of the interior angles, multiply the number of triangles by 180.

Which of these methods could be used to find the sum of the interior angles of the polygon below?

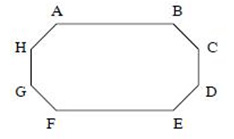
A. Multiply 8, the number of sides, by 180
Incorrect. The number of triangles formed by the diagonals from one vertex is always 2 less than the number of sides, 8, in the polygon. In this case 6 triangles are formed by the diagonals from one vertex, so you would have to multiply 6 by 180.

B. Multiply 6 by 180
Correct! The number of triangles formed by the diagonals from one vertex is always 2 less than the number of sides in the polygon. There are 8 sides and 6 triangles formed by the diagonals from one vertex, so you would have to multiply 6 by 180.

C. Divide 6 by 180
Incorrect. Multiply, not divide, 6 by 180.

D. Divide 360 by 8
Incorrect. This would be used to find each exterior angle of a regular octagon. To find the sum of the interior angles, multiply the number of triangles formed by the diagonals from one vertex (2 less than the number of sides - 8 sides and 6 triangles formed) by 180.

Lauren is making a tile pattern shown below for her kitchen. She has chosen regular hexagons as her primary tiles. She must have tiles shaped like parallelograms cut to fit in the spaces between the hexagonal tiles. In order to have the parallelogram-shaped tiles cut, she must find the measures of the angles, x and y for these tiles. What are the measures of angles x and y in this tile pattern?
  1. x = 120°; y = 120°
    supplementary
    Incorrect. Since x is an exterior angle of the hexagon, divide 360 by 6. The sum of the measures of the interior angles of a quadrilateral is 360 and adjacent angles are supplementary, therefore, subtract the measure of x from 180 to find the value of y.
  2. x = 90°; y = 90°
    Incorrect. You found the measure of one interior angle of a regular quadrilateral. This is not a regular quadrilateral To find x and y, x is the exterior angle of the regular hexagon and its measure is found by dividing 360 by 6, the number of sides in the hexagon. For this tile pattern, y is 120°, since the sum of the angles in any quadrilateral is 360° and adjacent angles of a parallelogram are supplementary: x + y = 60 + y = 180.
  3. x = 120°; y = 60°
    Incorrect. It appears that you thought that y was an exterior angle of a regular hexagon. To find x and y, x is the exterior angle of the regular hexagon and its measure is found by dividing 360 by 6, the number of sides in the hexagon. For this tile pattern, y is 120°, since the sum of the angles in any quadrilateral is 360° and adjacent angles of a parallelogram are supplementary: x + y = 60 + y = 180.
  4. x = 60°; y = 120°
    Correct! x is an exterior angle of the regular hexagon. Its measure can be found by dividing 360 by 6, the number of sides in the hexagon. For this tile pattern, y is 120°, since the sum of the angles in any quadrilateral is 360° and adjacent angles of a parallelogram are supplementary.

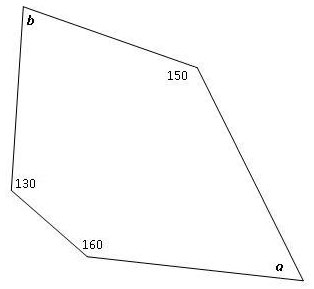
In the diagram below, find the sum of measures ∠a and ∠ b.

A. 100°
Correct! The sum of the angles in a pentagon is (n − 2)180 or 540°. The sum of the missing angles is 540 − (130 + 160 + 150) or 100°.

B. 240°
Incorrect. The sum of the angles in a pentagon is (n − 2)180 or 540°. The sum of the missing angles is 540 − (130 + 160 + 150) or 100°.

C. 146.67°
Incorrect. The sum of the angles in a pentagon is (n − 2)180 or 540°. The sum of the missing angles is 540 − (130 + 160 + 150) or 100°.

D. 140°
Incorrect. The sum of the angles in a pentagon is (n − 2)180 or 540°. The sum of the missing angles is 540 − (130 + 160 + 150) or 100°.