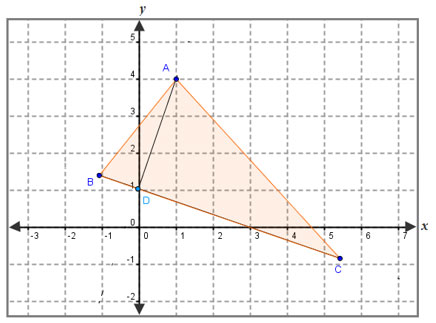
If AD is an altitude of △ABD, and y = 3x + 1 is the equation of the line containing AD, find the equation of the line containing base BC.

A. y = -3x + 1
Incorrect. The altitude is perpendicular to the base therefore the slopes are negative reciprocals. This answer is the negative of the given slope but it isn’t the reciprocal.

B. y = 1 3 x + 1
Incorrect. The altitude is perpendicular to the base therefore the slopes are negative reciprocals. This answer is the reciprocal of the given slope but it isn’t negative of the slope.

C. y = - 1 3 x + 1
Correct! The altitude is perpendicular to the base so the slopes of the equations must be negative reciprocals.

D. y = -x + 5
Incorrect. The altitude is perpendicular to the base therefore the slopes are negative reciprocals.

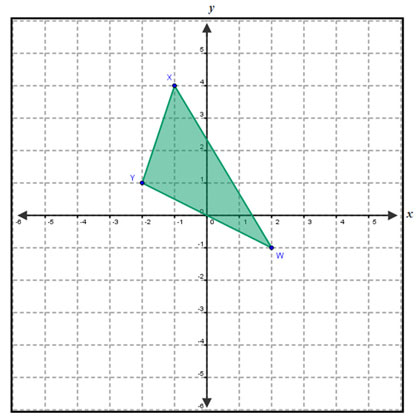
Determine the equation of the line containing side WX.

1. y = 3x + 7
   Incorrect. This is the equation containing side line segment XY.
2. y = - 5 3 x + 7 3
   Correct! The slope of the median is the negative reciprocal of the slope of the side.
3. y = -0.5x
   Incorrect. This is the equation containing side line segment XY.
4. y = 2x + 6
   Incorrect. This is the equation for the line that is perpendicular to line segment XY.

In ΔABC the vertices are as follows: A (15,1), B (9,11) and C (2,1). Find the coordinates of point M on AB so that CM is the median of ΔABC.

A. (6,12)
Incorrect. You have mixed up the x and y coordinates of your answer.

B. (5.5,6)
Incorrect. You found the midpoint of the wrong side of the triangle.

C. (12,6)
Correct! The median connects from the vertex to the midpoint of the side opposite.

D. (8.5,1)
Incorrect. You found the midpoint of the wrong side of the triangle.

In trapezoid ABCD, determine the coordinates that form the endpoints of the midsegment.

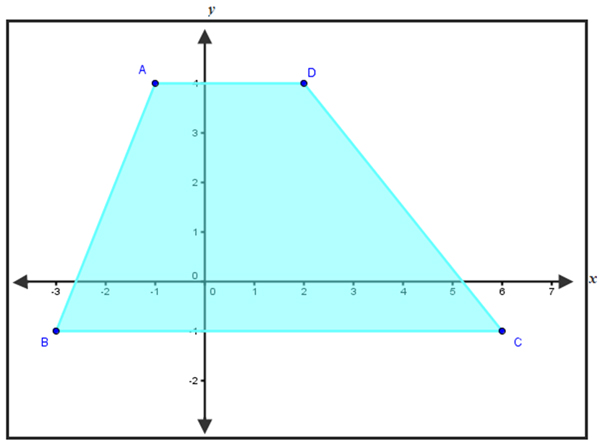
A. (0.5, 4) & (1.5, -1)
Incorrect. You have connected the midpoints of the parallel sides instead of the midpoints of the nonparallel sides.

B. (1.5, 4) & (1.5, -2)
Incorrect. You seem to have mixed up the x and y values in your coordinates.

C. (-1, 4) & (-1, 1)
Incorrect. You have found an altitude of trapezoid ABCD.

D. (-2, 1.5) & (4, 1.5)
Correct! You connected the midpoints of the nonparallel sides of the trapezoid to create the midsegment.