Two cereal boxes, in the shape of rectangular prisms, are similar, as shown below.

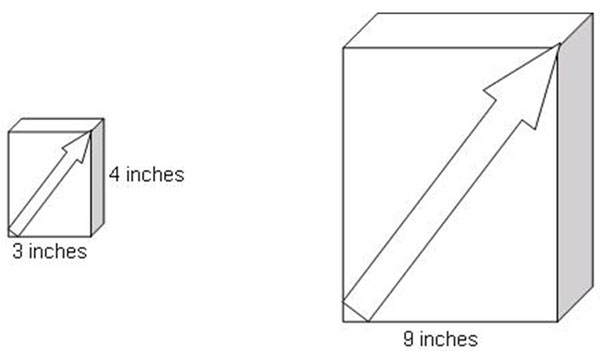
What is the length of the arrow on the front of the larger cereal box?

A. 5 inches
Incorrect. Find the scale factor from the smaller box to the larger box.

B. 12 inches
Incorrect. Find the Pythagorean triple for the smaller box first.

C. 15 inches
Correct! The front of the larger cereal box is a dilation of the front of the smaller cereal box, which has side lengths of a 3, 4, 5 Pythagorean triple.

D. 20 inches
Incorrect. Find the Pythagorean triple for the smaller box first.

Regular television sets have an aspect ratio of 4:3, meaning that the ratio of the length to the width of the rectangular screen is 4:3. If the screen of a regular television set has a length of 24 inches, what is the length of the diagonal of the screen?

A. 5 inches
Incorrect. Use the scale factor from the aspect ratio to the actual television set to find the diagonal of the screen.

B. 18 inches
Incorrect. Find the Pythagorean triple representing the ratio.

C. 30 inches
Correct! The screen is larger than the aspect ratio by a scale factor of 6 and the diagonal is the hypotenuse of the right triangle whose side lengths are represented by the Pythagorean triple 18, 24, 30.

D. 36 inches
Incorrect. Find the Pythagorean triple representing the lengths of the sides of a right triangle in the unit triangle for the aspect ratio.

A funicular is a rail car that is used to help pedestrians up a hill that is too steep to walk to the top. A particular funicular lifts a car full of pedestrains a vertical distance of 96 meters while covering a horizontal distance of 28 meters. What length of rail is required for the funicular to make this journey from the base of the hill to the top?

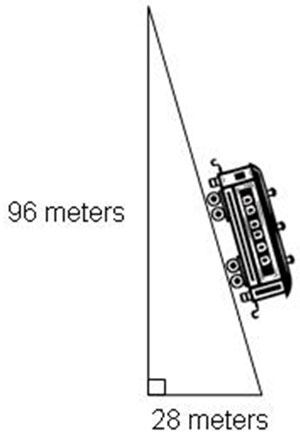
A. 124 meters
Incorrect. Find the Pythagorean triple by first finding the scale factor between 28 and 96, reduce and find the Pythagorean triple.

B. 64 meters
Incorrect. Find the Pythagorean triple by first finding the scale factor between 28 and 96, reduce and find the Pythagorean triple.

C. 25 meters
Incorrect. Find the Pythagorean triple by first finding the scale factor between 28 and 96, reduce and find the Pythagorean triple.

D. 100 meters
Correct! The funicular travels along the hypotenuse of a triangle whose side lengths are the Pythagorean triple 7, 24, 25 when multiplied by a scale factor of 4.

A ski lift brings novice skiers 500 meters up the mountain then drops them off to ski back down to the base. Veronica skis this route, and descends a vertical distance of 300 meters. A more advanced skier continues an additional 500 meters, then skis back down to the base. Rita skis this route, and descends a vertical distance of 600 meters. The diagram below shows a cross-section of the mountain on which Veronica and Rita are both skiing.

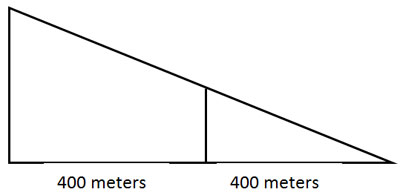
Which of the following is the best way to show that the triangle representing Veronica's ski path is similar to the triangle representing Rita's ski path?

A. Since Rita skied twice as far as Veronica, the triangles must be similar.
Incorrect. Draw the figure and label it. Find the scale factor relating the two triangles.

B. Since 300 + 600 is an equal sum to 400 + 500, the two triangles must be similar.
Incorrect. Draw the figure and label it. Find the scale factor relating the two triangles.

C. The triangle representing Rita’s ski path is a 300-400-500 triangle. The triangle representing Veronica’s ski path is also a 300-400-500 triangle. These are both dilations of a 3-4-5 right triangle.
Incorrect. Find the total lengths of the sides of the triangle representing Rita’s ski path.

D. The triangle representing Rita’s ski path is a 600-800-1000 right triangle. The triangle representing Veronica’s ski path is a 300-400-500 right triangle. These are both dilations of a 3-4-5 right triangle.
Correct! The triangles are both scaled from the same right triangle whose sides are a Pythagorean triples therefore they are similar by SSS similarity.