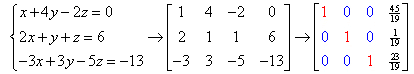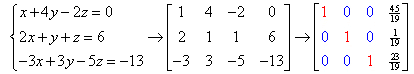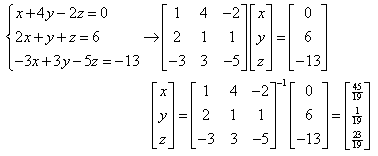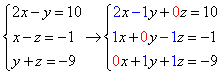Did you watch both videos, or did you decide ahead of time on a preferred method? Either solution strategy will work for almost any system, but there are a few more things to consider:

• If your system has three equations and three unknowns, you will solve it the exact same way, only the dimensions of matrices will be bigger.

Here is an example of a system of three equations with three unknowns using RREF to solve:

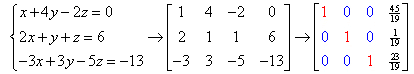
* Notice the placement of the 0’s and the diagonal of 1’s when the calculator changes the matrix to reduced row echelon form.

Or, here is the same system of three equations with three unknowns using an inverse matrix to solve:

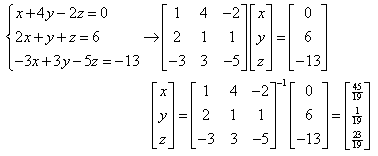
• If an equation is missing a variable, make sure you make the coefficient of that variable 0.
  

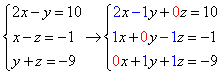
• If you are using an inverse matrix to solve a system with no solution or infinitely many solutions, you will get an error on your calculator because the coefficient matrix does not have an inverse.
  
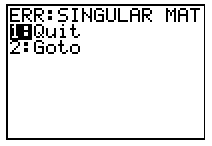
  Unfortunately, you won’t know if your system has no solution or infinitely many solutions, and you will have to resort to an algebraic solution (or use RREF) to solve the system.

• If you solve a system of equations using RREF that has infinitely many solutions, your last row will be all 0’s.
  
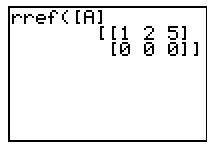
  You should interpret this as meaning 0x + 0y = 0; therefore, there are infinitely many values of x and y that would satisfy the system of equations.
• But if you try solving a system of equations using RREF that has no solution, the resulting matrix will look something like these examples.
  
  

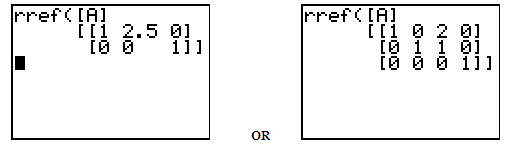
How should we interpret this? For the example on the left, the bottom row would mean 0x + 0y = 1. For any ordered pair (x, y), this is impossible. Therefore, there are no solutions to this system.