When either "h" or "k" is not zero, the ellipse will be translated to a position on the graph such that the center is not the origin. Identify the centers of the following ellipses:
Click on the blanks to check your answers.
x minus two squared over four (x − 2)2 4 + y squared over nine y2 9 = 1
Center: Interactive button. Assistance may be required. __________ (2, 0)
x squared over four (x)2 4 + y minus two squared over nine (y − 2)2 9 = 1
Center: Interactive button. Assistance may be required. __________ (0, 2)
x minus two squared over four (x − 2)2 4 + y plus three squared over 9 (y + 3)2 9 = 1
Center: Interactive button. Assistance may be required. __________ (2, -3)
x plus two squared over four (x + 2)2 4 + y minus three squared over nine (y − 3)2 9 = 1
Center: Interactive button. Assistance may be required. __________ (-2, 3)
Remember, the x-radius (major) and y-radius (minor) aren't affected by changes to h and k. For all ellipses above, the (major) x-radius = 2 and (minor) y-radius = 3.
How do we determine the location of the foci (focal points) on the ellipse?
a2 – b2 = c2 where 'c' is the focal radius (distance from the center to each focus, F1 and F2 below)
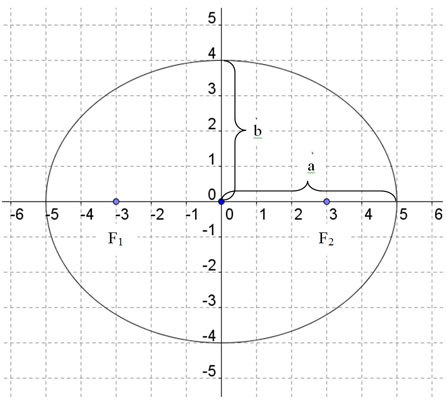
When you know the focal radius, c, you can locate the foci on the graph by “counting” from the center along the major axis in both directions the number of units of the radius. See the figure below and notice the locations of F1 and F2, the foci.

For this ellipse, the x-radius (5 units) is the major axis and the y-radius (4 units) is the minor axis. Therefore, a = 5 and b = 4 and a2 – b2 = 52 – 42 = 25 – 16 = 9 = c2. Then c = 3, the distance from the center to each of the foci. The foci are located at (-3, 0) and (3, 0).
Practice finding the focal radius for the following ellipses. Click the blanks to check your answers.