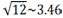 units.
units.Critical attributes for graphing an ellipse are: center, length of major radius, length of minor radius, and length of focal radius.
Here is an example of sketching the graph of an ellipse using x minus two squared over four (x − 2)2 4 + y plus three squared over sixteen (y + 3)2 16 = 1.
Center (2, -3), major radius (y-direction) = 4, minor radius (x-direction) = 2.
Focal radius2 = 42 – 22 = 16 – 4 = 12. So focal radius = 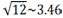 units.
units.
Step 1: Locate and plot the center point.
Step 2: Locate and plot points on major axis 6 units from center in either direction and on minor axis 4 units from center in either direction, as shown in the following figure.
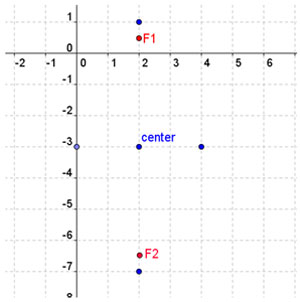
Step 3: Sketch in the curve of the ellipse through the four points on the major and minor axes as shown in the figure below.
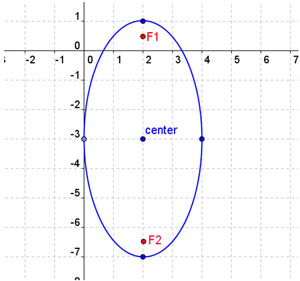
Notice the major axis of this ellipse is vertical because the radius in the y-direction is the longer.