As experienced in the first section, when graphing rational functions, you will encounter instances where the function cannot be defined.

What reason can you think of that may cause this to occur?

Interactive popup. Assistance may be required.

Check Your Answer

Since rational functions are defined as f(x) = Q(x) over P(x) Q(x) P(x) , if P(x) ever has a value of zero, then the function is undefined. Think of the parent function, f(x)= 1 over x 1 x . In this case, the function is undefined when x = 0.

Click on the image below to access the applet. The applet below will allow you to explore vertical asymptotes of graphs of rational equations using sliders.

Use the sliders to change the value of a and b in the function, x squared over (x + a)(x + b) x² (x + a)(x + b) . As you do so, notice how the vertical asymptotes are defined and how you might be able to find them given any rational function. Use the applet to complete the table below, and use your table to answer the conclusion questions that follow.

Interactive popup. Assistance may be required.

Need additional directions?

Interactive popup. Assistance may be required.

Check Your Answer

Values of a and b	Equations of Vertical Asymptotes
a = 3 b = -2	x = -3 x = 2
a = -5 b = 7	x = 5 x = -7
a = -6 b = 4	x = 6 x = -4
a = 6 b = -5	x = -6 x = 5

Conclusion Questions

Each time you changed the value of a or b, a vertical asymptote appeared on the graph telling you that the function could not be defined at that value of x. How could you find the equation of the vertical asymptote algebraically?

Interactive popup. Assistance may be required.

Check Your Answer

Since the value of the denominator can never be equal to zero, to find the equations of the vertical asymptotes simply set the denominator equal to zero and solve.

From the applet, if you have a value of a = 3, then what did that mean for the factor of the denominator and the corresponding vertical asymptote?

Interactive popup. Assistance may be required.

Check Your Answer

The value of a would give you a factor of (x + 3). However, this means that the corresponding vertical asymptote would be found at x = -3, which is the value of x where the function is undefined.

Pause and Reflect

The denominator of the rational function will give you the vertical asymptotes. Will there be rational functions that do not have vertical asymptotes or holes?

Interactive popup. Assistance may be required.

Check Your Answer

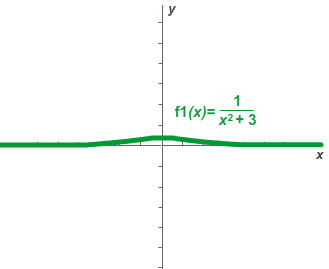
Since a rational function is a ratio of two polynomials, the polynomial in the denominator will tell you if there is a vertical asymptote. Yet, in some cases, there will not be a vertical asymptote. For example, in h(x) = 1 over x squared + 3 1 x² + 3 . When you set the denominator equal to zero and solve, you get an imaginary value for x. There is no value of x when substituted into the function that will cause the denominator to be zero and make the function undefined. The graph of this function is shown below.

When you are finding vertical asymptotes, you use the denominator of the function. Why is it important to also use the numerator in finding vertical asymptotes?

Interactive popup. Assistance may be required.

Check Your Answer

In some cases, you might have a common factor in both the numerator and denominator, which means there is a hole in the graph instead of a vertical asymptote.

Practice

1. Given the graph of the rational function below, what is the polynomial that represents the denominator?

Interactive popup. Assistance may be required.

Need a Hint?

Look at the vertical asymptotes. Remember how you used the equation for the vertical asymptote to work backward to a factor.

Interactive popup. Assistance may be required.

Check Your Answer

The denominator of the function would be (x − 2)(x − 3) or x² − 5x + 6.

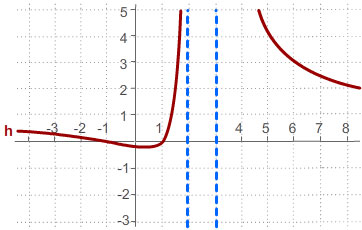
2. Identify the vertical asymptotes for the following function.

g(x) = 7x squared + 10x - 62 over x squared + 2x + 1 7x² + 10x − 62 x² + 2x + 1

Interactive popup. Assistance may be required.

Need a Hint?

Use the denominator to help you find the vertical asymptotes. If the numerator cannot be factored, then do not worry about holes in the graph.

Interactive popup. Assistance may be required.

Check Your Answer

x = -1

3. Which of the following statements are true regarding the rational function:

f(x) = x cubed + 7x squared + 12x over x cubed - 16x x³ + 7x² + 12x x³ − 16x

I. There is no vertical asymptote for f(x).
II. There is a vertical asymptote at x = 4.
III. There is a hole in the graph at x = -4.
IV. There is a hole in the graph at x = 0.

Interactive popup. Assistance may be required.

Need a Hint?

Factor the numerator and denominator of this rational function. You may need to factor out the greatest common factor from all three terms in each of the trinomials first.

Interactive popup. Assistance may be required.

Check Your Answer

Statements II, III, and IV are all correct.