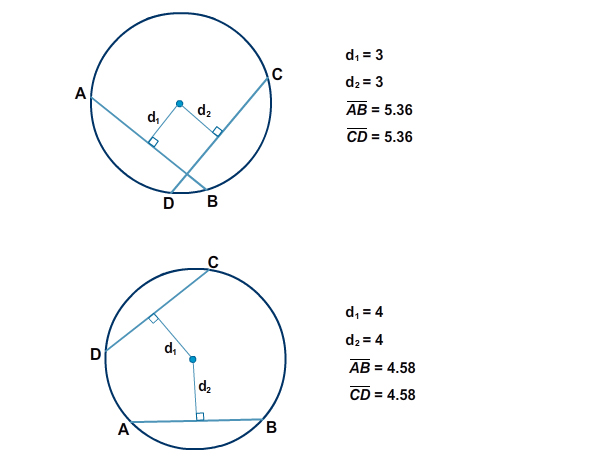
Review the congruent circles below.

1. Compare and contrast the two pictures.

Interactive popup. Assistance may be required.

Check your answer.

The chords are congruent and the d₁ and d₂ values are equal.

2. If two chords are the same distance from the center of a circle, then ____________________________________________________.

Interactive popup. Assistance may be required.

Check your answer.

If two chords are the same distance from the center of a circle, then the chords are congruent.

See if you can make up more conjectures on your own and add them to your journal. Consider using the intercepted arcs, central angles, etc. As an optional way to verify conjectures like this, you can print this page and use tracing paper to trace the congruent parts used in your conjectures.

I. Using the applet, Area Enclosed by Circle, drag the orange dot to change the value of r. Watch what happens to the values of the area.

Write at least two conjectures about the area and radius of a circle in your notes. Check for a possible answer below.

Interactive popup. Assistance may be required.

Check your answer.

Answers will vary but may include:
The area of a circle is equal to π * r².
The ratio of area:square of the radius is approximately equal to 3.14.

II. Using the activity Intersecting Chord Theorem, experiment with different lengths of chord AB by dragging the orange dot. Watch what happens to the chords. Write a conjecture for intersecting chords in a circle. Enter the conjecture into your notes. Answers will vary.

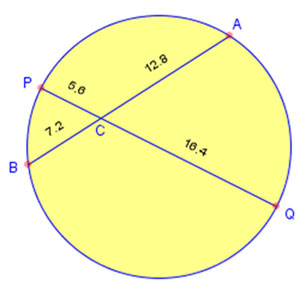
Source: Intersecting Chord Theorem, Math Open Reference