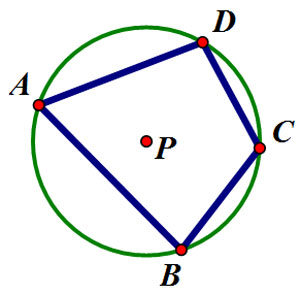
When a conjecture is made about a geometric figure, it means that someone applied some accepted truths to a new application.
In this conjecture about a quadrilateral inscribed in a circle, read the statements which support the conjecture.
For a quadrilateral inscribed in a circle, opposite angles are supplementary.

For example, in circle P, ∠A and ∠C are supplementary.
Click on the numbers below to see statements which can help support this conjecture:
The illustration shows a circle with an equation for circumference , C, using the ratio, r.

![]() Go to the activity Circumference, Perimeter of a Circle.
Go to the activity Circumference, Perimeter of a Circle.
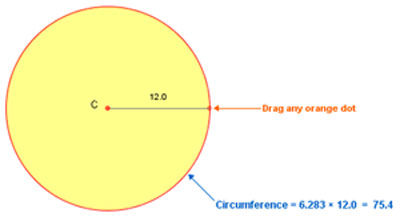
Source: Circumference of a Circle, Math Open Reference
Drag the orange dot to change the radius. Watch what happens to the circumference.
Complete each conjecture:
In a circle, for any ratio value, the ratio of the : 2 * is equal to approximately , commonly known as . In a circle, the is equal to π * * .

Understanding the circumference of a circle can lead to other conjectures. Recall that a circle can actually be measured in two different ways: by degrees and by circumference (or distance around the circle).
Complete the following and copy the statements into your journal.
1. A full circle is always degrees.
2. The distance around a circle is times its radius or π times its .

"Part" of a circle is called an arc. An arc has a degree measure and a length. The degree measure is a portion of 360°. For example, half of a circle (called a semicircle) would have a degree measure which equals half of 360°. So a semicircle arc always measures 180°. The circle below is divided into 12 equal sections. Find the degree measure of each arc indicated.
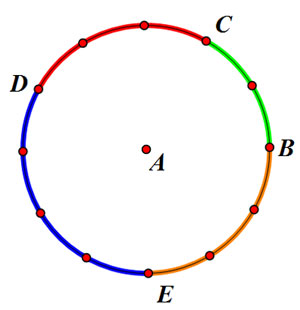
m = , m
= , m = , m
= , m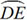 = , m
= , m =
=
Conjecture: The arc length can be found using a proportion: degree measure over 360 equals arc length over 2 times pi times the radius degree measure 360 = arc length 2πr
For the two circles shown, m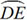 = 120 but one circle has a radius of 4 and the other circle has a radius of 12.
= 120 but one circle has a radius of 4 and the other circle has a radius of 12.
Find the arc length for 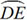 in each circle.
in each circle.
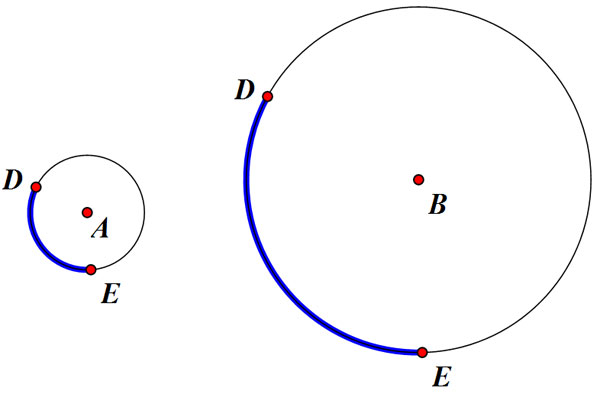
Circle A: Length of 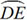 →
120
360
=
x
2π(4)
→
120
360
=
x
2π(4)
Circle A: Length of 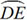 =
=
Circle B: Length of 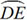 →
120
360
=
x
2π(12)
→
120
360
=
x
2π(12)
Circle B: Length of 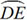 =
=
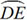 →
120
360
=
x
2π(4)
→
120
360
=
x
2π(4)
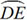 =
=
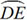 →
120
360
=
x
2π(12)
→
120
360
=
x
2π(12)
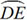 =
= 
More circle/arc conjectures:
How many conjectures can you write about circles and arcs? Write several in your journal, then check the resource section to see if you match any of those that have already been written.
As an extra challenge, consider what new conjectures can be written when you look at the following: