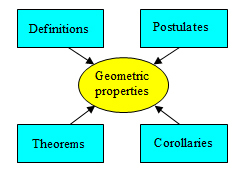
Geometry is made up of a vast structure of true statements, including definitions, postulates, and theorems and their corollaries.

Properties of geometric figures are supported by these statements. We rely on our knowledge of this structure so that we can make observations about what we see in the world around us.

For a list of definitions, postulates, and theorems, you can check out these websites:

Theorems and Postulates for Geometry

Mr. Combs's Geometry Postulates & Theorems

For example, a builder must know properties of lines, angles, and polygons in order to perform certain tasks. The photo shows the layout for a deck.

The builder uses the Pythagorean Theorem of right triangles to ensure that the layout lines are at right angles. He/she can also measure the diagonals of the rectangular layout to see if they are equal because of the geometry theorem that says the diagonals of a rectangle are congruent.

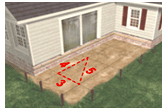
Source: Deck, easy2diy.com

Be sure to check your layout for square using the 3-4-5 right triangle method. Or, you can check for square by measuring from opposite corners and comparing the dimensions. They should be equal.

Knowledge of geometric properties gives you the power to make conjectures (statements) about whatever situation you are in and will help you solve problems.