Now you will investigate and prove some conjectures about chords in a circle. Suppose you have a circle containing 2 parallel chords.

Click on the "Begin Animation" button below and look for relationships. What do you notice about the intercepted arcs?

Copy the following in your notes, filling in the blanks. Click on the blanks to reveal the answers.

The measure of the first arc is Interactive button. Assistance may be required. _________ 50° and the measure of the second arc is Interactive button. Assistance may be required. _________ 50° .

Conjecture: If a circle contains parallel chords, those chords intercept Interactive button. Assistance may be required. _________ congruent arcs.

Now let's prove the conjecture.

Complete the following drag and drop puzzle to prove that this conjecture is true. Use the pictures to help you organize the statements and reasons in your proof. Use the Reset button to reset the puzzle if necessary.

Practice

Use circle K with parallel chords AD and BC, shown below, to answer questions 1-3.

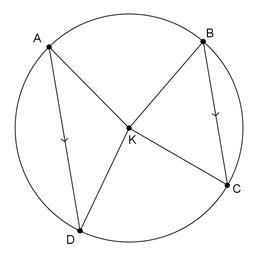
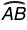1. If m = 83°, what is m 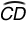? How do you know?

   Interactive popup. Assistance may be required.

   Need a hint?

   How are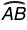 and 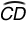related to the two parallel chords?

   Interactive popup. Assistance may be required.

   Check Your Answer

   m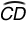 = 83° because two arcs intercepted by parallel chords are congruent, and congruent arcs have equal measures.

2. Kyoki studied circle K and wrote down several conjectures. Which of the following conjectures will always be true?
   1. AD ≅ BC
   2. ≅
   3. ∠AKD ≅ ∠BKC
   4. ∠AKB ≅ ∠CKD

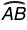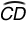
   Interactive popup. Assistance may be required.

   Need a hint?

   Which two arcs are intercepted by parallel chords?

   Interactive popup. Assistance may be required.

   Check Your Answer

   Conjectures II and IV only
   Conjecture I may or may not be true since we are not given information about the lengths of each chord.
   Conjecture III may or may not be true since central angles are not always congruent.

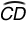3. Patti measured ∠AKB with a protractor and recorded that m∠AKB = 78.5°. What is m? How do you know?

   Interactive popup. Assistance may be required.

   Need a hint?

   How does m∠AKB relate to its intercepted arc?

   Interactive popup. Assistance may be required.

   Check Your Answer

   m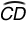 = 78.5°. ∠AKB is a central angle that intercepts 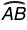, so m 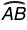= m∠AKB = 78.5° because a central angle has an angle measure that is equal to the measure of the intercepted arc. 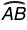≅ 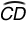because they are intercepted arcs of parallel chords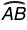. m = m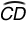 because congruent arcs have equal measures, so m 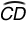= 78.5°.