In this section, you will make conjectures about chord lengths within a circle, and then use deductive reasoning to verify those conjectures.

Click on each chord below to place it in the circle. What do you notice about the chords?

• What do you notice about the length of each chord as compared to the distance from the chord to the center of the circle?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The longest chord is the diameter, which passes through the center of the circle. The farther away from the center a chord is located, the shorter the chord becomes.

• Is it possible to have a chord that is longer than the diameter? Why or why not?

  Interactive popup. Assistance may be required.

  Check Your Answer

  No. Any segment longer that the diameter would have at least one endpoint outside the circle.

Let’s use our observations to make a conjecture about two chords that would be the same length in a circle.

In your notes, complete the following conjecture.

Two chords in the same circle are congruent if they are Interactive button. Assistance may be required. _________. equidistant from the center.

Let's use deductive reasoning to prove it. You can have two congruent chords that are not necessarily parallel.

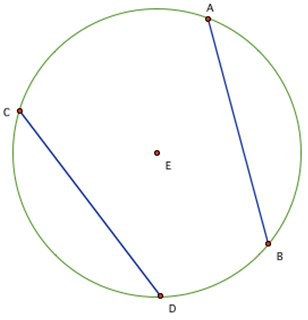
You can draw 4 radii: CE, DE, AE and BE.

Complete the following drag and drop puzzle to make a deductive argument to show congruent chords in the same circle are equidistant from the center of that circle. Use the Reset button to reset the puzzle if necessary.

Altitudes EG and EF are formed from Point E, the center of the circle, to CD and AB. Remember, that altitudes form right angles. The logical argument below proves that the altitudes are congruent.

Click each step to view the proof.

Looking at the diagram above, note that EG and EF both form 90° angles and cut the segments in half. This makes them not only medians and altitudes, but also Interactive button. Assistance may be required. _________. perpendicular bisectors.

There is more information you can prove from congruent chords. Remember, you showed that when you include the radii from the endpoints of the chords, you have isosceles triangles.

Complete the following drag and drop puzzle to discover another congruent chord relationship.

Pause and Reflect

In the first two interactives, you deductively proved the conjecture, "If two chords are congruent then they are equidistant from the center of the circle." Is the converse of this statement also true? If not, draw a counterexample.

Interactive popup. Assistance may be required.

Check Your Answer

The converse of this statement is also true. It can be deductively shown by using congruent triangles to show that the chords, which are corresponding parts of congruent triangles must be congruent.

Practice

Use circle Z, shown below, with CZ = DZ to answer Questions 1 and 2.

1. If LM = 14.4 centimeters, what is PN? How do you know?

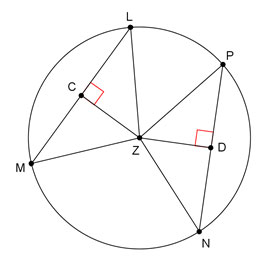
   Interactive popup. Assistance may be required.

   Need a hint?

   What do you know about the distance from each chord to the center of the circle?

   Interactive popup. Assistance may be required.

   Check Your Answer

   PN = 14.4 centimeters. Since CZ = DZ, CZ ⊥ LM, and DZ ⊥ PN, LM and PN are equidistant from the center of circle Z. Because LM and PN are equidistant from the center of circle Z, they are congruent chords and LM ≅ PN. Congruent segments have equal lengths, so LM = PN = 14.4 centimeters.

2. Janet studied circle Z and wrote down several conjectures. Which of the following conjectures will always be true?
   1. LM ≅ PN
   2. ≅
   3. ∠LZM ≅ ∠PZN
   4. ≅

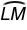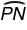
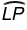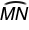
   Interactive popup. Assistance may be required.

   Need a hint?

   Since CZ = DZ, what does that reveal about the distance between the center of the circle and chords LM and PN?

   Interactive popup. Assistance may be required.

   Check Your Answer

   Conjectures I, II, and III only
   Conjecture IV may or may not be true since we are not given information about the distance between the center of the circle, point Z, and chords LP and MN.