Let's say that you are given the following information:

• Supplementary angles are 2 angles whose sum is 180°.
• ∠A and ∠B are supplementary angles.
• m∠A = 5x - 5 and m∠B = 4x + 20.

Which of the following statements is true concerning ∠A and ∠B? Justify your answer.

1. m∠A = m∠B
2. m∠A = 2( m∠B)
3. m∠A > m∠B
4. m∠A < m∠B

Interactive popup. Assistance may be required.

Check Your Answers

1. False.   m∠A = 120° and the m∠B = 60°.
2. True.   m∠A = 120° and the m∠B = 60°.
3. True.  m∠A = 120° and the m∠B = 60°, so m∠A > m∠B.
4. False.  m∠A = 120° and the m∠B = 60°, so m∠A > m∠B.

In the diagram below:

• Lines p and q are parallel.
• Line t is a transversal that passes through p and q.
• m ∠a = 5x and the m ∠b = 3x - 12

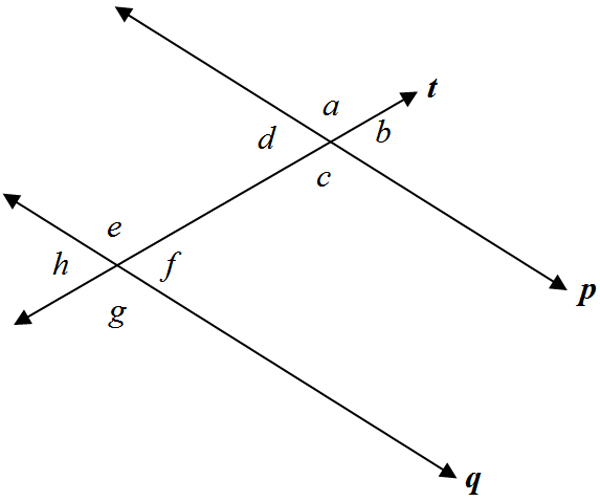
Which of the following statements are valid? Justify your answer.

1. ∠a and ∠b are supplementary angles.
2. m∠a = m∠c
3. m∠d = m∠h
4. ∠e and ∠f are complementary angles.
5. ∠c and ∠g are corresponding angles.
6. m∠h = 24°

Interactive popup. Assistance may be required.

Check Your Answers

1. True. These angles form a linear pair.
2. True. These angles are a pair of vertical angles.
3. True. These angles are corresponding angles.
4. False. These angles are supplementary angles, not complementary angles.
5. True. These angles are corresponding angles since they are located on the same side of the transversal and situated the same way on the parallel lines.
6. False.  m∠h = 60° (the value of x = 24°) The m∠h = m∠d (corresponding angles). The m∠d = m∠b (vertical angles). Therefore, the m∠h = m∠b = 60°.