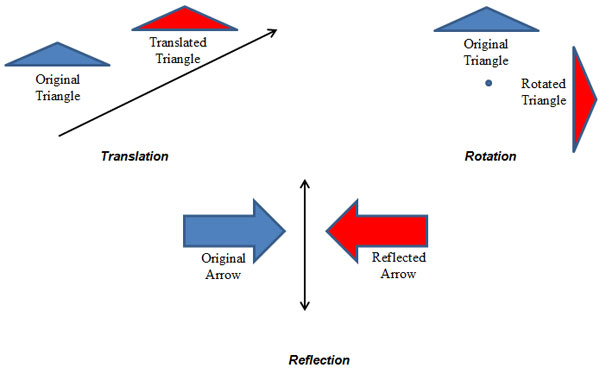
An isometry is a transformation that preserves distance, which means that the pre-image and the image are congruent. An isometry is also called a congruence transformation.

The etymology for isometry is from two Greek root words: iso, meaning “same,” and meter, meaning “measure.”

Three of the basic transformations are isometries; translation, rotation, and reflection.

Some isometries can be generated using a sequence of other isometries.

Translations – Reflections Across Two Lines

In the figure below, figure Z is reflected across two parallel lines to generate Zʹʹ. Let’s examine each step to discover how this could be the case!

Recall: A Interactive button. Assistance may be required. ___?___reflection can be thought of as a mirror image.

• Pre-image Z is Interactive button. Assistance may be required. ___?___reflected over line l to generate image Zʹ.
• Image Zʹ is Interactive button. Assistance may be required. ___?___reflected over line m to generate image Zʹʹ.
• Lines l and m are Interactive button. Assistance may be required. ___?___parallel .
• The pre-image Z was reflected two times.
  
  
• The pre-image Z is Interactive button. Assistance may be required. ___?___ translated to image Zʹʹ.

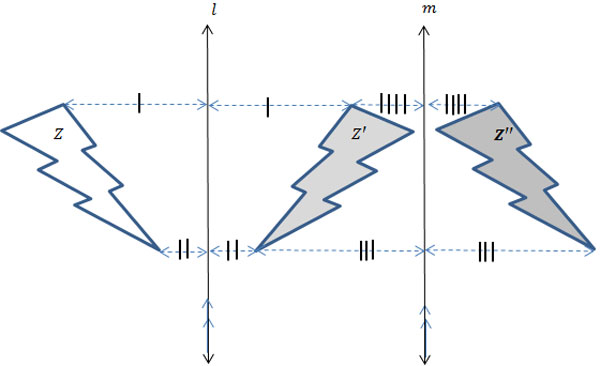
Translational symmetry occurs when a pre-image is reflected twice, creating an image Interactive button. Assistance may be required. ___?___translated from the pre-image.