Source: Pyramid Arena, Exothermic, Flickr

Recall from the lesson introduction that the Pyramid Arena is a regular rectangular pyramid in Memphis, Tennessee.

Suppose that Marshall has been contracted to resurface the exterior of the Pyramid Arena using solar electricity panels. Before he can start, he needs to know exactly how much material it will take for him to resurface this regular pyramid.

Before beginning, let’s examine the problem situation more closely.

• Will Marshall need to calculate the total surface area of the pyramid or the lateral surface area? How do you know?

  Interactive popup. Assistance may be required.

  Need a hint?

  Which faces of the pyramid will Marshall be resurfacing with solar electricity panels?
  Interactive popup. Assistance may be required.

  Check Your Answer

  Marshall will need to calculate the lateral surface area because he will only be resurfacing the lateral faces of the pyramid.
• Which area formulas will Marshall need to use in order to make his calculations?

  Interactive popup. Assistance may be required.

  Need a hint?

  What shape(s) are the lateral faces of the pyramid?
  Interactive popup. Assistance may be required.

  Check Your Answer

  Since the lateral faces are all triangles, Marshall will need to use the area formula for a triangle, A = 1 over 2 1 2 bh.
• What dimensions of each triangular face will Marshall need to know in order to calculate the area of each face?

  Interactive popup. Assistance may be required.

  Need a hint?

  What do the variables b and h stand for in the triangle area formula?
  Interactive popup. Assistance may be required.

  Check Your Answer

  Marshall will need to know the base length, b, and the height, h, of each triangular face of the pyramid.
• To which dimension of the pyramid does the height of the triangular lateral face compare?

  Interactive popup. Assistance may be required.

  Need a hint?

  A pyramid has an altitude height, which is the vertical distance from the apex to the base of the pyramid. It also has a slant height, which is the perpendicular distance from the apex to the base edge along the triangular lateral face.
  Interactive popup. Assistance may be required.

  Check Your Answer

  The slant height of the pyramid is the same as the height of the triangular lateral face.

Marshall is provided the height of the Pyramid Arena, 321 feet, and the length of each base edge of the pyramid, 590 feet, as shown in the diagram below.

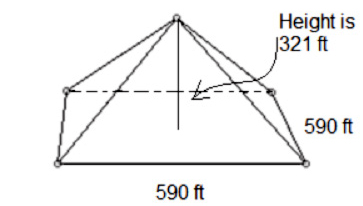
In most problem situations, the slant height of a pyramid will be given. However, sometimes, as in the situation with Marshall and the Pyramid Arena, you will have to find the slant height using the information given in the problem.

Watch the video below to see how the slant height can be calculated when you know the height of the pyramid and the base edge length.

The images below summarize how the slant height was calculated in the video.

Using the side view of the pyramid, you see that the height of the pyramid is perpendicular with the base.

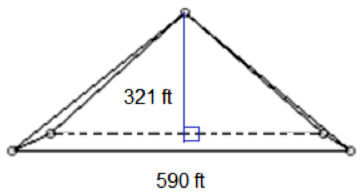
Therefore, a right triangle is created. Its hypotenuse is the slant height of the pyramid. Using the Pythagorean Theorem with the height and half of the length of the base as the legs of the right triangle, you can calculate the slant height.

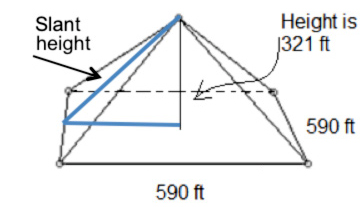
Using the Pythagorean Theorem and rounding to the nearest whole number value, the slant height is calculated to be about 436 feet.

Next, let's look at the Pyramid Arena as a net with all of the measurements that you know now.

• What is the area of each triangle in the net?

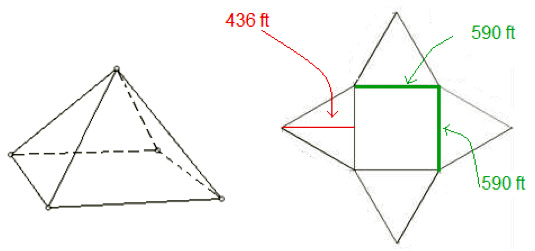
  Interactive popup. Assistance may be required.

  Need a hint?

  Use the triangle area formula, A = 1 over 2 1 2 bh.
  Interactive popup. Assistance may be required.

  Check Your Answer

  A = 1 over 2 1 2 bh
  A = 1 over 2 1 2 (590 ft)(436 ft)
  A = 128,620 ft²
• What is the complete area that Marshall will need to resurface?

  Interactive popup. Assistance may be required.

  Need a hint?

  Which faces of the pyramid will Marshall need to resurface? Determine the sum of the areas of these faces.
  Interactive popup. Assistance may be required.

  Check Your Answer

  Surface Area = 4 × Area of One Triangle
  
  Surface Area = 4 × 128,620 ft²
  
  Surface Area = 514,480 ft²
• If solar electricity panels cost $25 per square foot, then what will be the total cost to completely cover the surface of the Pyramid Arena with solar electricity panels?

  Interactive popup. Assistance may be required.

  Need a hint?

  How much will 1 square foot cost? 2 square feet?
  Interactive popup. Assistance may be required.

  Check Your Answer

  Total Cost = $25 per ft² × Surface Area
  
  Total Cost = 25 × 514,480 = $12,862,000

Pause and Reflect

How could nets help you determine the surface area of other figures?

Interactive popup. Assistance may be required.

Check Your Answer

If you know the net of a figure and its dimensions, then you can calculate the area of the relevant faces of the figure.

Practice

For each of the figures below, determine the total surface area.

Interactive popup. Assistance may be required.

Need a hint?

What shapes are the faces that are present in each net? What are the area formulas that you can use to determine the area of each of those shapes?

1.

2.

Interactive popup. Assistance may be required. Check Your Answer This net is a triangular prism, which has two congruent triangular bases and 3 rectangular lateral faces. Area of Base =1 over 2 1 2 bh = 1 over 2 1 2 (3.5 cm)(3 cm) = 5.25 cm2 Area of Lateral Faces = bh + bh+ bh = (8.6 cm)(3.5 cm) + (8.6 cm)(3.5 cm) +(8.6 cm) (3.5 cm) = 30.1 cm2 + 30.1 cm2 + 30.1 cm2 = 90.3 cm2 Surface Area = Area of Bases + Area of Lateral Faces = 2(5.25 cm2) + 90.3 cm2 = 100.8 cm2

Interactive popup. Assistance may be required. Check Your Answer