Although finding the sum of the areas of each face of a three-dimensional object will give you both the lateral and total surface area, finding the surface area becomes more efficient when you can generalize this process using a formula. In Geometry module 3, lesson 2, you worked with the surface area of a cone using its net.
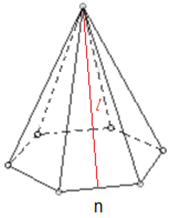
Now, let's explore the net of a regular hexagonal pyramid to see the connection of measurements on the solid and how the formula for surface area of a pyramid is found. In the following image and animation, n is the side length of the regular hexagon and l is the height of the isosceles triangle that forms the lateral surface of the pyramid.

Answer the following two questions before viewing the animation.
Interactive popup. Assistance may be required.
Each triangle base has a length of n.
Interactive popup. Assistance may be required.
The total length of all of the bases of the triangles is: n + n + n + n + n + n = 6n, which is the perimeter of the base.
![]()
Now that you have all of the dimensions labeled on the net, use the net to answer the following questions.
Interactive popup. Assistance may be required.
A = 1 over 2 1 2 nl
View the animation to see how to find the area of all the triangles.
![]()
Now that you have the expression for the total area of the isosceles triangles, A = 1 over 2 1 2 nl + 1 over 2 1 2 nl + 1 over 2 1 2 nl + 1 over 2 1 2 nl + 1 over 2 1 2 nl + 1 over 2 1 2 nl, how will the perimeter of the base, n + n + n + n + n + n = 6n, that you found earlier help you to simplify the expression for the total area of the isosceles triangles?
Use the animation below, which shows you how you can factor out the common factor of 1 over 2 1 2 l from each term in the expression for total area of the lateral faces, or isosceles triangles.
![]()
Interactive popup. Assistance may be required.
What values are common to both of the equations that you are trying to combine?
Interactive popup. Assistance may be required.
What type of faces of the pyramid are the isosceles triangles?
Most formula charts will show you that the formula for the lateral surface area of a pyramid is:
A = 1 over 2 1 2 Pl
In this formula, P represents the perimeter of the base of the pyramid and l represents the slant height of the pyramid.
What additional information is needed to find the total surface area of the solid?

How would this information be shown in the formula?
Determine the total surface area of each of the figures represented by the nets shown below.
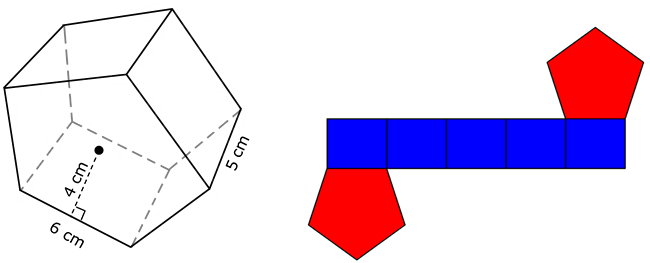
Interactive popup. Assistance may be required.
What shapes are present in the net? What are the area formulas for those shapes?
Interactive popup. Assistance may be required.
| The figure is a pentagonal prism, so determine the area of the 2 congruent triangular bases and the area of the 5 rectangular lateral faces. | Area of base: A = 1 over 2 1 2 Pa A = 1 over 2 1 2 (5(6 cm))(4 cm) A = 1 over 2 1 2 (30 cm)(4 cm) A = 60 cm2 |
Area of lateral face: A = bh A = (6 cm)(5 cm) A = 30 cm2 |
Total surface area = 2 × 60 cm2 + 5 × 30 cm2 = 270 cm2 |

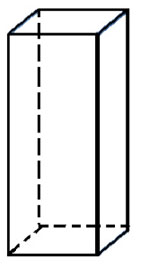
In the rectangular prism shown to the right, the area of the square base is 225 square inches and the height of the prism is 42 inches. What is the total surface area of the prism?
You may use the applet from this lesson to construct the net of the prism. If you choose to do so, here are some directions that you may find to be helpful.
![]()
 A Plethora of Polyhedra Applet
A Plethora of Polyhedra Applet
Interactive popup. Assistance may be required.
Construct a net of the figure. What shapes are present in the net? What are the area formulas for those shapes?
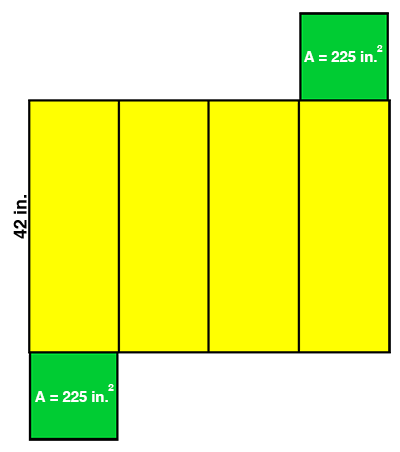
Because the base is a square and its area is 225 square inches, the side length of the
base is √225 = 15 inches.
