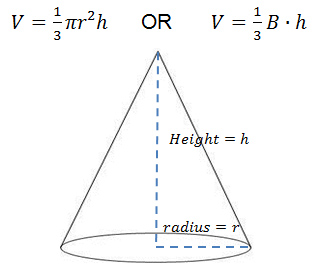
The amount of space occupying a cone or volume is related to the volume of a cylinder. The base is a circle like the base of a cylinder, except different sizes of circles are put one on top of the other to find the volume.

How do the volumes compare if the area of both bases (B) and both the heights (h) are the same? This applet will illustrate the difference in the volume of a cylinder and cone with the same base and height. In the bottom left hand corner, select Cone -> Tank.

Refer to the applet to answer the following questions. Click on the blanks to reveal the answers.

• The radii of both the bases are Interactive popup. Assistance may be required. __________ equal .
• Both bases have the same Interactive popup. Assistance may be required. __________ area .
• The heights of the cylinder and cone are Interactive popup. Assistance may be required. __________ equal .

Move the slider next to the cylinder to predict the height the liquid will be when poured from the cone into the cylinder.

• Write down your prediction. Interactive popup. Assistance may be required. __________ answers will vary

Click on the Pour button to transfer the liquid from the cone to the cylinder.

• How does the answer compare to your prediction? Interactive popup. Assistance may be required. __________ answers will vary
• Did the liquid from the cone fill the cylinder? Interactive popup. Assistance may be required. __________ No

Using the blue arrow next to the cylinder, slide the marker to the top of the liquid to see how the volume of the liquid from the cone compares to the volume of the cylinder. What did you discover? Interactive popup. Assistance may be required. __________ The volume of the cone is about 1 3 the volume of the cylinder.

Click the New Problem button.

• The radius and height for both the cylinder and the cone are Interactive popup. Assistance may be required. __________ equal .
• Move the slider and predict the outcome. Interactive popup. Assistance may be required. __________ The liquid from the cone will fill 1 3 the cylinder.

The volume of a cone is 1 3 the volume of a cylinder.

Compare a cylinder and a cone by answering the following questions. Click on the blanks to reveal the answers.

• A cylinder is the same size and shape from top to bottom. Any cross-section of a cylinder is a Interactive popup. Assistance may be required. __________ circle that is congruent to the bases. A cone has one circular Interactive popup. Assistance may be required. __________ base at the bottom and the top or the opposite end is a point.
• The base of the cylinder and the base of the cone are both Interactive popup. Assistance may be required. __________ circles with an area of Interactive popup. Assistance may be required. __________ A = πr² .
• The formula for the volume of a cylinder is Interactive popup. Assistance may be required. __________ V = πr² ⋅ h or V = B ⋅ h . The formula for the volume of a cone is Interactive popup. Assistance may be required. __________ V = 1 3 πr²h or V = 1 3 Bh . The only difference between the two formulas is the Interactive popup. Assistance may be required. __________ 1 3 in the formula for the volume of a cone.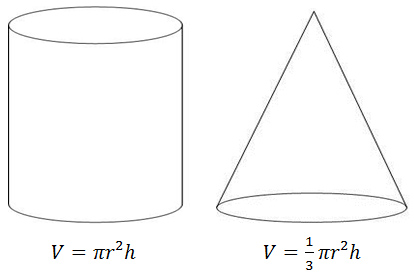

Since the circles are different sizes and have different areas the formula for a cone is: