In this section, you are going to continue investigating quadrilaterals that have unique characteristics.
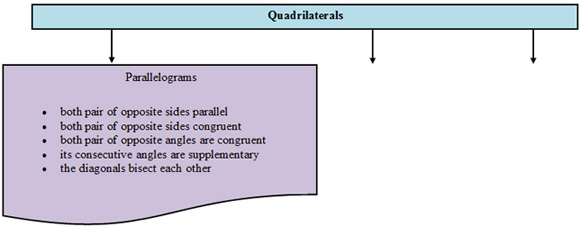
A parallelogram is a quadrilateral that has:
Now that you understand parallelograms, you can start working on the flow chart for quadrilaterals. You can fill in what you know so far about parallelograms.

![]()
Look at the parallelogram below.
Let’s think about what properties would need to be present to know that this parallelogram is also a rectangle.
By definition, a rectangle is a parallelogram with four right angles. With this in mind, let’s see what our rectangle would look like:
You could say that a rectangle is always a parallelogram, but a parallelogram is not always a rectangle.
![]()
 Using this applet, http://www.mathopenref.com/rectanglediagonals.html:
Using this applet, http://www.mathopenref.com/rectanglediagonals.html:
In your notes, answer the following questions from the Investigate section:
Knowing that a rectangle is a parallelogram, what are two important properties of the diagonals of a rectangle? Use a picture to illustrate your response.

So, you know that a rectangle is always a parallelogram, but a parallelogram is not always a rectangle. Not bad! Rectangles are easy! Let’s add rectangles to our quadrilateral flow chart:
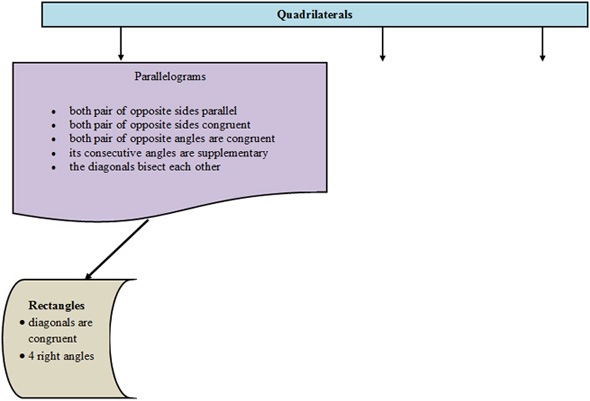
An important property of a rectangle that is different from other parallelograms is that the diagonals of a rectangle are congruent.
This means that if you have a parallelogram with congruent diagonals then you know the parallelogram is a rectangle.
If you are given ![]() ABCD and you are given that AC = 24 and BD = 3(2x-5), what value of x would be necessary in order to prove that
ABCD and you are given that AC = 24 and BD = 3(2x-5), what value of x would be necessary in order to prove that ![]() ABCD is a rectangle?
ABCD is a rectangle?
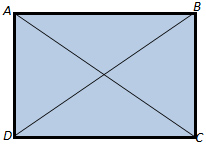
First things first! If ABCD is a rectangle, then AC ≅ BD. That means that AC = BD.
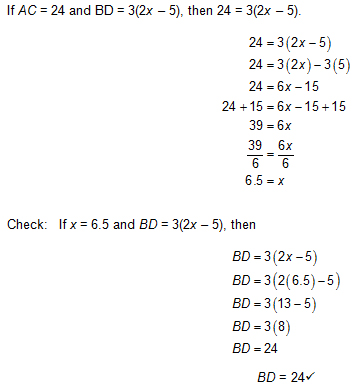
Conclusion: If x = 6.5, then BD = 24 and AC ≅ BD. This means that ![]() ABCD is a rectangle since the diagonals are congruent.
ABCD is a rectangle since the diagonals are congruent.