 Open this applet, http://www.mathopenref.com/kite.html:
Open this applet, http://www.mathopenref.com/kite.html:In this lesson, we are going to take a close look at trapezoids and kites. Let’s start with a focus on the kite.
![]()
 Open this applet, http://www.mathopenref.com/kite.html:
Open this applet, http://www.mathopenref.com/kite.html:
In your notes, answer the questions below. You can check your answers by clicking on each blank.







Good going! Let's add kites to our quadrilateral flow chart.
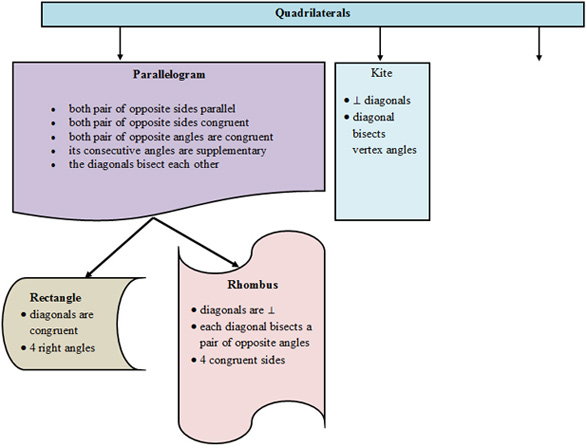
Time for our last quadrilateral! Let's talk about trapezoids.
A trapezoid is a quadrilateral with exactly one pair of parallel sides. The parallel sides are called the bases of the trapezoid. The nonparallel sides are called legs of the trapezoid. In this figure, AB and CD are the bases of the trapezoid.
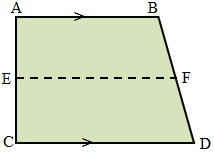
Base angles of a trapezoid are pairs of angles whose common sides are a base of the trapezoid.
∠A and ∠B are base angles and ∠C and ∠D are base angles of trapezoid ABCD. The segment that joins the midpoint of the two legs is called the midsegment of the trapezoid. EF is the midsegment of the figure above.
Let's investigate some relationships involving the midsegment of a trapezoid.

![]() Open this applet http://www.mathopenref.com/trapezoidmedian.html, and move each point around individually to observe the trapezoid.
Open this applet http://www.mathopenref.com/trapezoidmedian.html, and move each point around individually to observe the trapezoid.
In your notes, answer the following questions:



The midsegment of a trapezoid is parallel to each base of the trapezoid and it's length is one-half the sum of the lengths of the two bases.
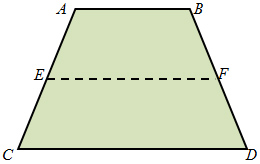
This theorem is telling us that EF || AB and EF || CD.
It also tells us that EF = AB + CD 2
Another way to write the formula for finding EF is 2(EF) = AB + CD.

Let's move on to Isosceles Trapezoids.
A special trapezoid is one in which the legs of the trapezoid are congruent. Trapezoid ABCD at the right is an isosceles trapezoid since the two legs, AC and BD are congruent.
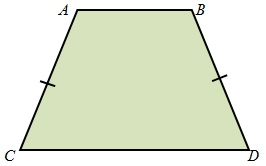
Let's look at a few facts about an isosceles trapezoid.
Trapezoid Theorem 1: If a quadrilateral is an isosceles trapezoid, then each pair of base angles are congruent.
For Trapezoid ABCD above, this means that ∠A ≅ ∠B and ∠C ≅ ∠D.
The converse of this theorem, Trapezoid Theorem #2, provides a way to prove that a trapezoid is an isosceles trapezoid.
Trapezoid Theorem 2: If a trapezoid has one pair of congruent base angles, then the trapezoid is isosceles.
With this information, if you know that Quadrilateral TRAP is a trapezoid and you know that ∠P ≅ ∠A, then we also know TRAP is an isosceles trapezoid.
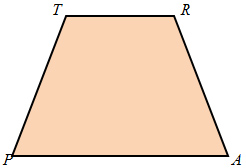
Now for our last isosceles trapezoid theorem.
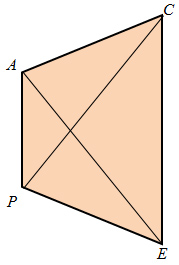
Trapezoid Theorem 3: A trapezoid is isosceles if, and only if, its diagonals are congruent.
This means that if you have Trapezoid PACE and know that PC ≅ AE, then you can be confident that Trapezoid PACE is isosceles.
With all of this information, let's sum up what you know about an isosceles trapezoid.
Let's add the trapezoid information to our quadrilateral flow chart.
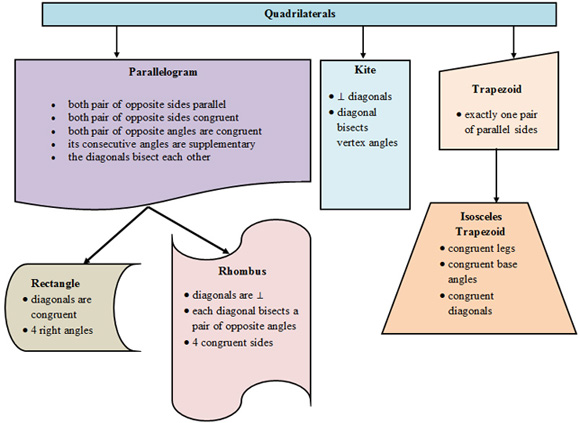
Now that you have completed the quadrilateral flow chart, click here for a printable chart. Print it out so that you have it with you in your geometry notebook.