Click on the image below to access the applet. In Geometry module 1, lesson 10, you had the opportunity to make and test conjectures regarding the length of a chord within a circle. Additionally, in that lesson, you were able to make and test conjectures on the corresponding arc lengths formed by chords as well as the use of chords in constructing the circle relationships within a circle. If you would like to review that information before moving forward, see module 1, lesson 10 of this course.
In this section of the lesson, you will investigate the following three properties of chords in a circle:
First, let’s investigate the relationship between a chord and the radius of a circle to which it is perpendicular. To do so, let's use the applet below.
Click on the image below to access the applet.
In the applet, click and drag point A to the inside of the circle. Then, click and drag point B until OB, the radius of the circle, is perpendicular to chord CD (it will turn red and a perpendicular mark will appear). To change the size of the circle, hold down the Shift key while you click and drag the circumference of the circle. Use the interactive to collect four different data points that you can use to complete the table and answer the questions below.
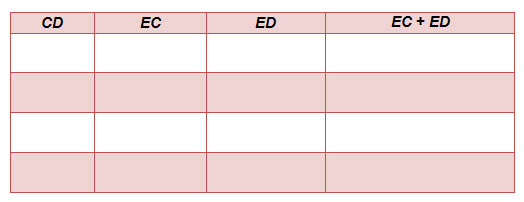
Interactive popup. Assistance may be required.
EC + ED = CD
Interactive popup. Assistance may be required.
A radius that is perpendicular to the chord bisects the chord.
Interactive popup. Assistance may be required.
Radius OB is a perpendicular bisector to chord CD.
Interactive popup. Assistance may be required.
If a radius is perpendicular to a chord, then it will bisect the chord.
Now that you have discovered the relationship between a chord and the radius to which it is perpendicular, let's use that property to explore the relationship between the length of congruent chords and their distance from the center of the circle. To accomplish this task, watch a short video clip taken from the Wolfram Demonstrations Project.
Click on the image below to access the video.
As you're watching the video, notice the two congruent chords in the circle. As the chords are manipulated, watch for what happens to the distance from the center of the circle to each chord. Also watch to see the relationship between the segment of the radius and the chord.
Use what you observed in the video to answer the questions below.
Interactive popup. Assistance may be required.
The distances from the center of the circle to each congruent chord are equal.
Interactive popup. Assistance may be required.
No. Parallel chords never intersect, and even when the chords intersected, the distances represented by OA and OB remained equal.
Interactive popup. Assistance may be required.
If two chords are congruent, then they are equidistant from the center of the circle.
Now, you will investigate and describe the relationship between two chords that intersect inside a circle. To do so, use the interactive applet below.
Click on the image below to open the applet and investigate the Intersecting Chords Theorem. On the circle, click and drag any of the orange dots around the circle. Manipulate all four points on the circle.
In your notes and using the circle below, formalize the Intersecting Chords Theorem by answering the questions below.
Interactive popup. Assistance may be required.
Each chord is cut into two parts by the intersection point of the two chords. The product of the lengths of two parts of one chord is equal to the product of the lengths of the two parts of the other chord.
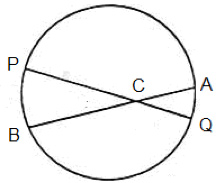
Interactive popup. Assistance may be required.
(AC)(CB) = (PC)(CQ)
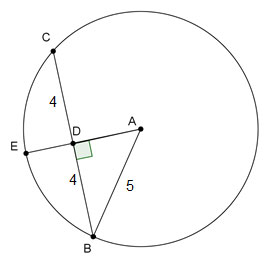
Use the figure below to answer questions 1 and 2.
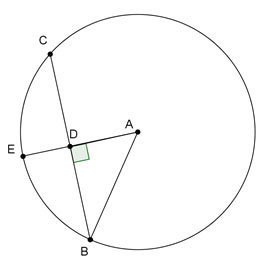
Interactive popup. Assistance may be required.
What is the relationship between BC and AE?
Interactive popup. Assistance may be required.
Since radius AE is perpendicular to chord BC, BD = DC = 1 over 2 1 2 BC.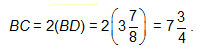
Interactive popup. Assistance may be required.
In a circle, all radii are congruent. Since radius AE is perpendicular to chord BC, it bisects BC.
Interactive popup. Assistance may be required.
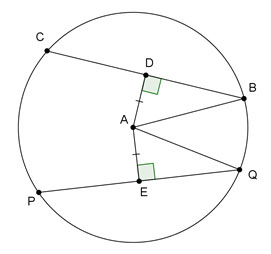
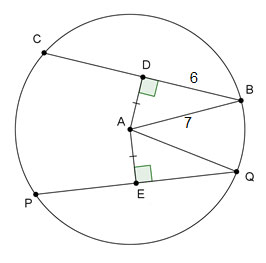
Use the figure below to answer questions 3 and 4.
Interactive popup. Assistance may be required.
Chords that are equidistant from the center of a circle are congruent. The radius that is perpendicular to the chord bisects that chord.
Interactive popup. Assistance may be required.
PQ = BC, so BC = 12 inches.
Interactive popup. Assistance may be required.
The distance between chord BC and the center of the circle is represented by AD .
Interactive popup. Assistance may be required.
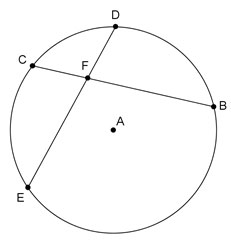
Use the figure below to answer questions 5 and 6.
Interactive popup. Assistance may be required.
If two chords intersect each other, then the products of the lengths of the two parts of each chord are equal.
Interactive popup. Assistance may be required.
EF(FD) = CF(FB)
Interactive popup. Assistance may be required.
If two chords intersect each other, then the products of the lengths of the two parts of each chord are equal.
Interactive popup. Assistance may be required.
EF(FD) = CF(FB)
