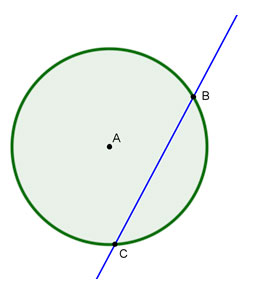
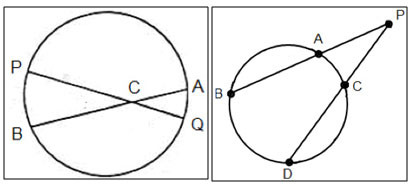
A secant of a circle is a line that intersects the circle in two points. In circle A, is a secant because it intersects the circle at point B and again at point C.

Can a line ever intersect a circle at more than two points? What about fewer than two points? Use the interactive applet below to determine an answer to these questions.

Click on the image below to access the applet.

In the applet, click and drag an orange point to move the secant line around the circle.

In your notes, explain the difference between a secant and a chord.

Interactive popup. Assistance may be required.

Check Your Answer

A chord is a segment with both endpoints on the edge of a circle, while a secant is a line that intersects the circle at two points. However, the interior section of a secant will form a chord.

As with chords, there is a special relationship when two secants intersect outside of a circle.

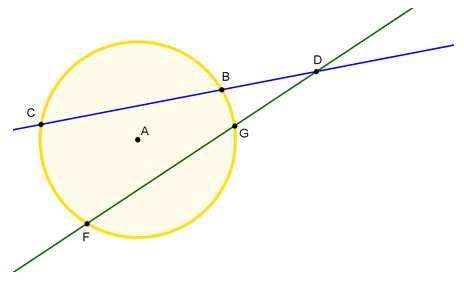
In circle A, there are two secants, and 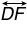, that intersect each other at point D. There are four segments created between the point of intersection of the two secants, point D, and the points where each secant intersects circle A.

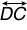: DB and DC
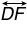: DG and DF

Click on the image below to access the applet.

In the applet below, click and drag an orange dot to investigate relationships among segments created by two intersecting secants to a circle.

Interactive popup. Assistance may be required.

Need additional directions?

Use what you observed in the applet to answer the questions below.

• How does the product of the length of a segment formed by the intersection of two secants and the intersection of one secant with the circle multiplied by the length of the segment formed by the point of intersection of the secants and the other intersection of that secant with the circle compare to the product of lengths of the corresponding parts for the other secant line?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The two products are equal.

• Use the circle below to write an equation representing the relationship that you discovered while manipulating the applet.
  

  Interactive popup. Assistance may be required.

  Check Your Answer

  (PA)(PB) = (PC)(PD)

Pause and Reflect

A chord is the portion of the secant line that lies within the circle. How does the formula from the Intersecting Secants Theorem, used when the point of intersection lies outside the circle, compare with the formula from the Intersecting Chords Theorem, used when the point of intersection lies inside the circle?

Interactive popup. Assistance may be required.

Check Your Answer

The product of the lengths of the two segments on a secant (or chord) formed by the intersection of two secants (or chords) to the two intersections of the secant (or chord) and the circle is equal to the product of the lengths of the corresponding segments of the other secant (or chord). In this aspect, the formulas are alike.

Practice

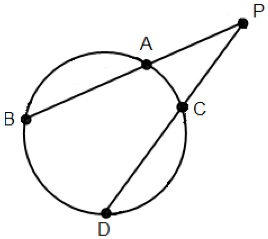
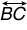1. In the diagram below, and 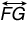are two secants of circle A that intersect at point D.
   

   What is DF?

   Interactive popup. Assistance may be required.

   Need a hint?

   The product of the length of the segment between the intersection of two secants and the closer intersection of the circle multiplied by the length of the segment formed by the intersection of the secants and the farther intersection with the circle is equal to the product of the lengths of the corresponding segments for the other chord or secant.

   Interactive popup. Assistance may be required.

   Check Your Answer

   DB(DC) = DG(DF)
   You are given the lengths of DB, DG, and BC, so you need to determine the length of DC in order to use the Intersecting Secants Theorem.
   DC = DB + BC
   DC = 8 + 17
   DC = 25
   
   DB(DC) = DG(DF)
   8(25) = 10(DF)
   1 over 2 8(25) 10 = DF
   20 = DF

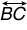2. In the diagram below, and 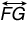are two secants of circle A that intersect at point D, BC is a diameter of circle A, and BC = 23.
   

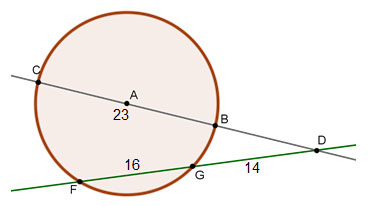
   What is DB?

   Interactive popup. Assistance may be required.

   Need a hint?

   The products of the exterior segment (the segment between the intersection of the secants and the closer intersection of the circle) and the long segment (the segment between the intersection of the secants and the farther intersection of the circle) for each secant are equal.

   Interactive popup. Assistance may be required.

   Check Your Answer

   DB(DC) = DG(DF)
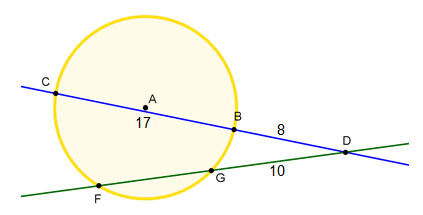
   You are given the lengths of DB, DG, and FG, so you need to determine the length of DF in order to use the Intersecting Secants Theorem.
   DF = DG + GF
   DC = 14 + 16
   DC = 30
   
   You need to determine the length of the exterior segment, so let DB = x.
   DB(DC) = DG(DF)
   x(x + 23) = 41(30)
   x² + 23x = 420
   x² + 23x – 420 = 0
   (x – 12)(x + 35) = 0
   x = 12, -35
   DB = 12

   

3. A lake that is roughly circular will have a bridge built from point B to point C. A 25-foot rope is stretched from point F to point G, and the line is extended to point D so that DG = 40 feet.
   

   If DB is measured to be 26 feet, how long will the bridge be?

   Interactive popup. Assistance may be required.

   Need a hint?

   The products of the exterior segment (the segment between the intersection of the secants and the closer intersection of the circle) and the long segment (the segment between the intersection of the secants and the farther intersection of the circle) for each secant are equal.

   Interactive popup. Assistance may be required.

   Check Your Answer

   DB(DC) = DG(DF)
   You are given the lengths of GF, DG, and DB, so you need to determine the length of DF in order to use the Intersecting Secants Theorem.
   DF = DG + GF
   DF = 40 + 25
   DF = 65
   
   BC represents the portion of the long segment that is inside the circle, so let BC = x, and the long segment will be x + 26.
   DB(DC) = DG(DF)
   26(26 + x) = 40(65)
   676 + 26x + 2600
   26x = 1924
   x = 74
   
   The bridge will be 74 feet long.