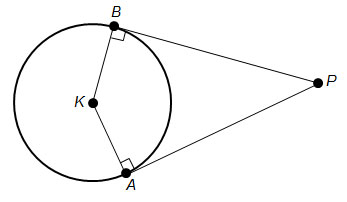
A tangent to a circle is the line that intersects the circle at one point on the circle. The point of intersection is called the point of tangency. This is critical because a radius drawn to a point of tangency is always perpendicular to the tangent line.

You will use an interactive applet to investigate this property and make an important conjecture about tangent lines and tangent segments.

Use the interactive below to investigate the relationship between two tangent segments that are drawn to a circle from a common exterior point. Click and drag point B to resize the circle, and click and drag point C to move the exterior point.

Use what you observed in the applet to answer the questions below.

• What do you notice about the lengths of the two tangent segments that are drawn from exterior point C?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The lengths of the two segments are equal, so the two segments are congruent.

• Use the circle below to write an equation representing the relationship that you discovered while using the applet.
  

  Interactive popup. Assistance may be required.

  Check Your Answer

  PA = PB

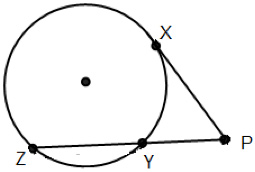
You have explored what happens when the chords of a circle intersect, when the secants of a circle intersect, and when the tangents to a circle intersect. Based upon this knowledge, what do you think the relationship is between the intersection of a secant line and a tangent of a circle as drawn below?

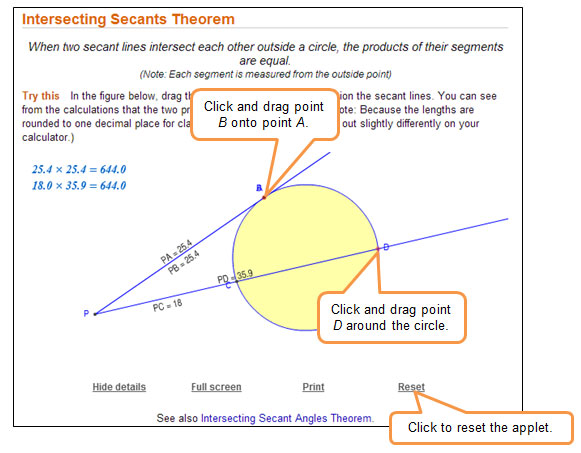
In order to explore this situation, the Secant-Tangent Product Theorem, let's use the applet linked below. It is the same applet we used to discuss the Intersecting Secant Theorem.

In the applet, in order to make a tangent appear, move point B on top of point A. What you should have, then, is PA and PB with the same measured lengths. In short, you will have a line that only touches the circle at one point, or a tangent. Move point D around the remainder of the circle and observe the values of the product.

Interactive popup. Assistance may be required.

Need additional directions?

Use what you observed in the applet to answer the questions below.

• Since PA was equal to PB, was it still being multiplied? How?

  Interactive popup. Assistance may be required.

  Check Your Answer

  PA and PB are still being multiplied. Since the values are equal, the length of the tangent segment is being multiplied by itself, or squared.

• What is the relationship between the length of the tangent segment and the lengths of the two segments formed by the intersections of the tangent with the secant and the circle?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The length of the tangent segment squared is equal to the product of the two segments of the secant line formed by the intersection point with the tangent and the intersection points with the circle.

• Use the circle below to write an equation representing the relationship that you discovered while manipulating the applet.
  

  Interactive popup. Assistance may be required.

  Check Your Answer

  XP² = PY(PZ)

Pause and Reflect

How does the Secant-Tangent Product Theorem compare to the Intersecting Secants Theorem?

Interactive popup. Assistance may be required.

Check Your Answer

The Intersecting Secants Theorem tells you that if two secants intersect outside the circle, then the products of the two sets of secant segments (external secant segment and entire secant segment) are equal. The Secant-Tangent Product Theorem is a special case of this relationship, when one set of secant segments (external secant segment and entire secant segment) become the same and are called a tangent segment.

Practice

1. In circle A below, if CD = 25, what is the length of DE?
   

   Interactive popup. Assistance may be required.

   Need a hint?

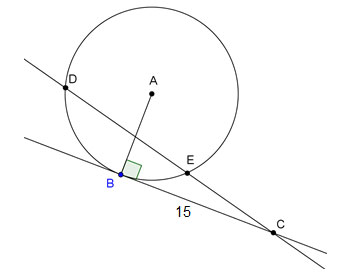
   The length of the tangent segment squared is equal to the product of the two secant segments (external secant segment and entire secant segment).

   Interactive popup. Assistance may be required.

   Check Your Answer

   CE(CD) = BC²
   You are given the lengths CD and BC, so you need to determine the length CE in order to calculate the length DE.
   CE(CD) = BC²
   CE(25) = 15²
   CE = 9
   
   The Segment Addition Postulate relates CE, ED, and CD.
   CE + ED = CD
   9 + ED = 25
   ED = 16
   
   ED is the same as DE, so DE = 16.

2. In the diagram below, RS = 14 and SP = 28.
   

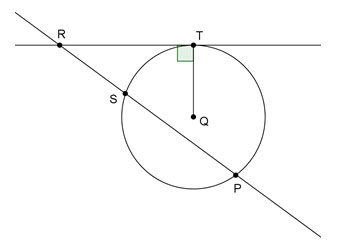
   What is RT?

   Interactive popup. Assistance may be required.

   Need a hint?

   The length of the tangent segment squared is equal to the product of the two secant segments (external secant segment and entire secant segment).

   Interactive popup. Assistance may be required.

   Check Your Answer

   You are given the lengths RS and SP, so you need to determine the length RP in order to use the Secant-Tangent Product Theorem.
   RP = RS + SP
   RP = 14 + 28
   RP = 42
   
   RP = 42
   RS(RP) = RT²
   14(42) = RT²
   588 = RT²
   √588 = RT
   14√3 = RT