In a previous lesson, you investigated different ways to determine the area of composite figures. Composite figures are combinations of polygons and other planar figures that do not have unique area formulas. Instead, to determine the area of these figures, you must first determine the polygons or circular regions for which you do have area formulas and then break the composite figure down into those regions.

One composite figure involving circles is a segment of a circle. A segment of a circle is the region between a chord of a circle and its associated arc.

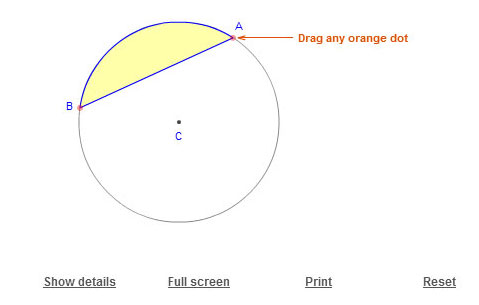
Use the interactive below to explore segments of circles. Click and drag on any orange dot to change the size and shape of the segment.

Interactive popup. Assistance may be required.

Need additional directions?

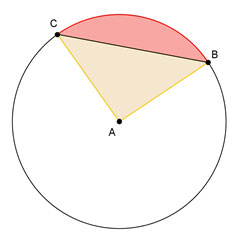
As you have seen by using the interactive for segments of circles, the two endpoints of a segment can be connected to the center of the circle to create a radius. In the diagram shown at the right, circle A contains chord BC and sector CAB. The chord divides the sector into two regions.

Use the interactive below to assemble an equation that describes the relationship between the area of a sector and the area of its related segment.

Click on the shape you'd like to place in the first box.

Use your equation from the interactive to answer the conclusion questions below.

• Write a sentence relating the area of the sector of the circle, the area of the segment of the circle, and the area of the triangle formed by the two radii of the sector and the chord.

  Interactive popup. Assistance may be required.

  Check Your Answer

  The area of the sector is equal to the sum of the area of the segment and the area of the triangle formed by the two radii and the chord.

• How could you use this information to calculate the area of the segment of a circle?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Calculate the area of the sector and the area of the triangle, and then subtract the area of the triangle from the area of the sector.

Practice

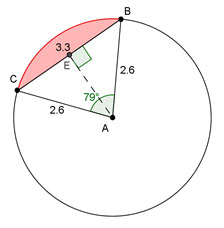
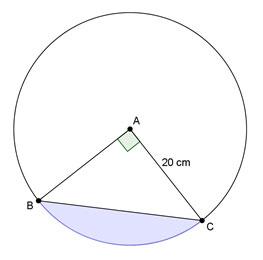
Determine the area of the shaded region in each figure below.

1. In circle A, the radius is 2.6 units, m∠CAB = 79°, and BC = 3.3 units.
   
   
   
   Interactive popup. Assistance may be required.

   Need a hint?

   Determine the area of the sector and the area of the triangle. To determine the area of the triangle, you need to know the base and height, which are two perpendicular segments. Use AE ⊥ BC, and use the Pythagorean Theorem to determine AE.
   Interactive popup. Assistance may be required.

   Check Your Answer

   
2. In circle A below, AC = 20 centimeters and AB ⊥ AC.
   
   
   
   Interactive popup. Assistance may be required.

   Need a hint?

   Determine the area of the sector and the area of the triangle. To determine the area of the triangle, you need to know the base and height, which are two perpendicular segments. Use AB ⊥ AC, and since these two radii of the circle are congruent, ΔABC is a 45-45-90 right triangle.
   Interactive popup. Assistance may be required.

   Check Your Answer