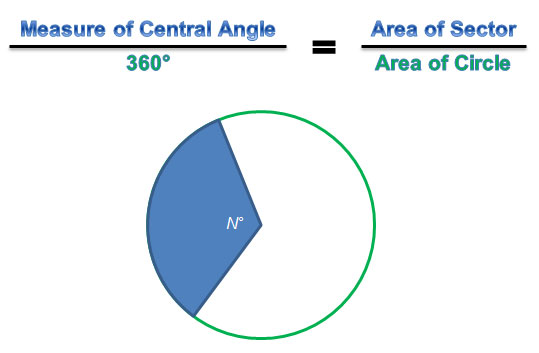
In this lesson, you used proportional reasoning to relate the area of a sector of a circle to the area of the entire circle.

Once you have the proportion relating the ratio of the measure of the central angle to the measure of a full circle and the ratio of the area of a sector to the area of the full circle, you can rearrange this proportion in order to solve for different variables, depending on the information that is given in any problem.

If N represents the measure of the central angle, and r is the radius of the circle, then you can simplify this equation to one that is commonly seen in textbooks.

You can also use this relationship in order to determine the area of parts of a circle, such as the segment of a circle. A segment of a circle is created when a sector of a circle, which is the region between two radii, is sliced by a chord connecting the two endpoints of the radii that were used to create the sector.

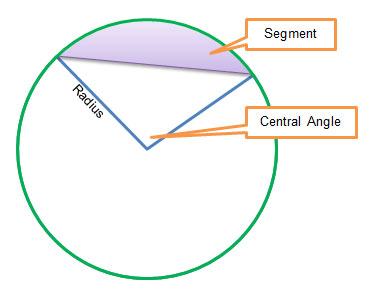
To determine the area of a segment of a circle, you can treat the problem like a composite area problem, where the area of the segment is the difference between the area of the sector and the area of the triangle that has been removed from the sector.