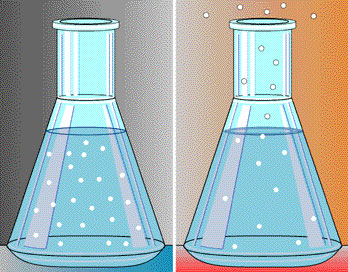
Source: Cool and heated gas, NOAA
Warm air is less dense and rises while cool air is denser and sinks. Look at the diagram below. Imagine that the circles in the Erlenmeyer flasks are air molecules. The image on the left shows the molecules when the air is cool, and the image on the right shows the molecules when heated. When the molecules are heated, they move faster and move apart, causing them to be less dense and rise.

Source: Cool and heated gas, NOAA
When the warm air rises and the cool air sinks, convection currents are created. Since gas molecules are not visible, it is hard to imagine convection currents. If you place food coloring in the bottom of a container and apply heat under the food coloring, you can see convection currents in action. Watch this video below to see a demonstration of convection currents.
![]()
Source: Convection Current Demo, Telsclear, YouTube

Wind is the moving of air and is created by differences in air pressure. The greater the differences in air pressure, the faster the wind moves. The differences in air pressure are caused by the unequal heating of Earth. If you have ever watched the weather, you know that the Earth does not heat evenly. In the summers in Texas, the temperatures can be well above 100°F, while in the northern states, the temperatures are in the 70s. Due to the tilt of the Earth, the air around the equator is consistently warmed. This warm air is less dense and rises. As the air rises, it creates an area of low pressure. At the poles, the air is colder and more dense so the air sinks. This cold, sinking air creates areas of high pressure. Pressure differences in the atmosphere cause the air to move. Winds generally move from the poles to the equator because air moves from areas of high pressure to areas of low pressure.
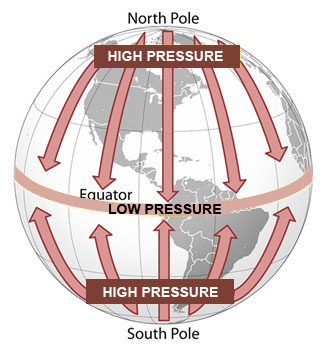
Source Adapted From: Earth, National Energy Education Development Project
The pattern of pressure is not as simple as the diagram above. As warm air rises, it begins to cool and eventually stops rising. Then some of the cool air begins to sink. This happens at about 30° north and 30° south latitude. This sinking air causes high pressure belts in these latitudes.
Cold air sinks at the poles. As the air moves away from the poles and along Earth's surface, it begins to warm and the pressure drops. This drop in pressure creates low pressure belts around 60° north and 60° south latitude. Convection cells, which are circular patterns of wind, are caused by this rising and sinking of air. The image below shows the convection cells.
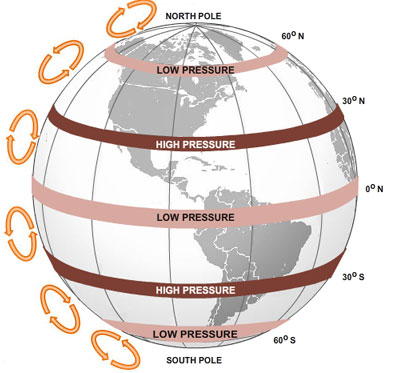
Source Adapted From: Earth, National Energy Education Development Project
 Directions: Complete the following statements by selecting the correct terms.
Directions: Complete the following statements by selecting the correct terms.