In this section, you will learn what causes an exponential or logarithmic graph to shift right or left.

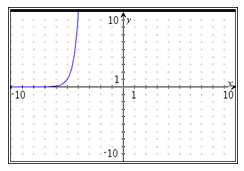
Below are four functions, four graphs, and four descriptions of translations to the graphs of some exponential and logarithmic functions. Some functions, graphs, and descriptions have already been placed in the table. Place the remaining functions, graphs, and descriptions in the correct place.

Conclusion Questions

• Which parameter appears to generate the horizontal translation?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The number that is being added or subtracted from x, the independent variable in the parent function, generates the horizontal translation.

• What do you notice about the sign of the parameter in each function and the direction of the translation?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The direction of the horizontal translation is the opposite of the sign of the parameter.

Pause and Reflect

How does the horizontal translation of exponential and logarithmic functions compare to the horizontal translation of other functions, such as quadratic, square root, or rational functions?

Interactive popup. Assistance may be required.

Check Your Answer

The horizontal translation of all functions works the same, regardless of the function family. The direction of the translation is the opposite of the sign of the term being added or subtracted from the independent variable, x. The distance of the translation is the same as the number being added or subtracted from the independent variable, x.

Practice

1. Describe the horizontal shift from the parent function for the function, r(x) = −6log(x – 9) – 3.

   Need a hint?

   Which parameter in the function controls the horizontal shift or horizontal translation of the graph of the function?

   Interactive popup. Assistance may be required.

   Check Your Answer

   The horizontal shift is 9 units to the right.

2. Describe the transformation of the graph of h(x) = 2^{x + 4} in order to generate the graph of
   p(x) = 2^{x –5}.

   Need a hint?

   Which parameter in the function controls the horizontal shift or horizontal translation of the graph of the function?

   Interactive popup. Assistance may be required.

   Check Your Answer

   The graph of h(x) would be shifted 9 units to the right of the graph of p(x).

3. What has happened to the equation k(x) = 10^x, to create p(x), the function whose graph is shown below?
   

   Need a hint?

   What would be the y-intercept of the graph of k(x)? Use that point to determine the transformation.

   Interactive popup. Assistance may be required.

   Check Your Answer

   k(x) = 10^x changed to p(x) = 10^x+5