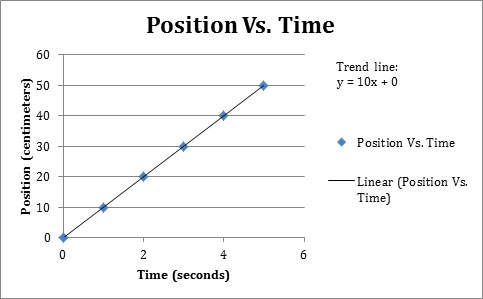
Two students are performing an investigation about the motion of a battery-powered car. Their results are summarized in the graph below.

Position vs. time graph including endpoints (0,0) and (5,50) and a trend line described by y = 10x + 0

What was the average velocity from t = 2 seconds to t = 4 seconds?

A. 10 cm/second
Correct! The slope of the line is the average velocity.

B. 20 cm/second
Incorrect. Twenty is the value of the position at 2 seconds. You need the change in position over the change in time.

C. 40 cm/second
Incorrect. Forty is the value of the position at 4 seconds. You need the change in position over the change in time.

D. 0 cm/second
Incorrect. Zero is the y-intercept, which is the initial position. You need the change in position over the change in time.

A car accelerates uniformly from rest to a velocity of 15 m/s over a displacement of 25 m. What is the value of the acceleration?

A. 0.6 m/s2
Incorrect. You divided velocity by displacement. You need an equation that solves for acceleration.

B. 3.3 m/s2
Incorrect. You have solved for the time. You need an equation that solves for acceleration.

C. 4.5 m/s2
Correct! The acceleration can be found using the constant acceleration equations.

D. 1.7 m/s2
Incorrect. This would have been the time if the car had been driving 15 m/s for the entire problem. You need an equation that solves for acceleration.

A student used a motion sensor located at the top of an inclined air track to measure the position and velocity of a glider as it moved down the track. As part of his data analysis, the student created a graph of his data, but forgot to include a title for the graph and labels for the axes.

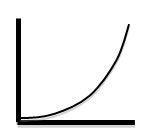
Graph without labels showing an upward parabolic curve

What would be the most appropriate title for this graph?

A. Velocity vs. Time
Incorrect. The Velocity vs. Time graph for motion with constant acceleration would be a line with positive slope.

B. Acceleration vs. Time
Incorrect. The Acceleration vs. Time graph for motion with constant acceleration would be a horizontal line.

C. Force vs. Time
Incorrect. The Force vs. Time graph for motion with constant acceleration would be a horizontal line.

D. Position vs. Time
Correct! This graph is parabolic, which corresponds to the Position vs. Time graph for motion with constant acceleration.

A car that is driving along the highway at a constant speed of 50 miles per hour passes mile marker 215 at 9:00 am. Which mile marker will the car pass at 11:30 am?

A. 125
Incorrect. This is the car’s displacement. The problem is asking for the final position.

B. 265
Incorrect. This is the mile marker that the car will pass after one hour. The car has been traveling for 2.5 hours.

C. 340
Correct! The car will travel 125 miles in 2.5 hours. Therefore the car will reach marker number 340.

D. 587.5
Incorrect. You multiplied the initial position by time and added the result to the velocity. You need to multiply velocity by time and add the result to the initial position.

A 1000 kg car is moving at 20 m/s when the driver applies the brakes. If the car is brought to rest in 80 meters, what is the magnitude of the average stopping force supplied by the brakes?

A. 2500 N
Correct! The force is found by multiplying the average acceleration by the mass of the car.

B. 20000 N
Incorrect. You have calculated momentum (mass × velocity), the question asks for force.

C. 2.5 N
Incorrect. This is the correct acceleration of the car. Now use Newton’s second law to determine the force.

D. 8000 N
Incorrect. You calculated the stopping time instead of the acceleration of the car. Try solving the time-independent equation for acceleration, and then use Newton’s second law to determine the force.

A worker is using a rope to pull a box across a rough floor. Using the information given in the free body diagram below, describe the motion of the box.

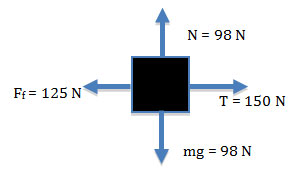
Force diagram showing tension to the right of 150 Newtons, friction to the left of 125 Newtons, normal force up of 98 Newtons, and weight down of 98 Newtons.

A. The box will accelerate to the left.
Incorrect. The tension is greater than the friction.

B. The box will move with constant velocity.
Incorrect. The right and left forces are not equal.

C. The box will remain stationary.
Incorrect. The right and left forces are not equal.

D. The box will accelerate to the right.
Correct! The tension is greater than the friction.

A child is tossing a ball straight up and down while riding a train. To an observer on the ground, the path of the ball while it is rising would be —

A. a straight vertical line
Incorrect. While the ball is moving up, it is also moving forward with the train.

B. a straight horizontal line in the same direction of the train
Incorrect. While the ball is moving forward with the train, it is also moving up.

C. a parabola curving forward with the motion of the train
Correct! The trajectory of the ball would be a parabola combining the upward motion of the ball with the forward motion of the train.

D. a diagonal line up and forward
Incorrect. The trajectory of the ball would be a parabola combining the upward motion of the ball with the forward motion of the train.

A CD is spinning as shown in the image below. If a point on the edge of the CD is moving with a constant speed of 180 cm/s, what is the centripetal acceleration at that point?

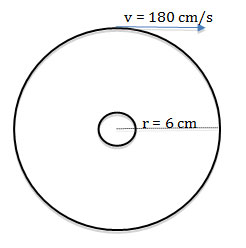
Compact disc with radius of 6 centimeters and speed at the edge of 180 centimeters per second.

A. 0 cm/s2
Incorrect. The tangential acceleration is 0 cm/s2, the question asks for the centripetal acceleration.

B. 5400 cm/s2
Correct! The velocity squared divided by the radius is 5400 cm/s2.

C. 30 cm/s2
Incorrect. You calculated the rotational velocity in radians/second.

D. 5 cm/s2
Incorrect. You calculated velocity divided by radius squared. You need to divide velocity squared by the radius.

Consider the situation of driving a nail onto a piece of wood with a hammer. When the hammer hits the nail, which of the following is an action-reaction pair?

A. The hammer pushes down on the nail, and the nail pushes down on the wood.
Incorrect. The objects described are not acting on each other.

B. The hammer pushes down on the nail, and the nail pushes up on the hammer.
Correct! The objects described are acting on each other with equal and opposite forces.

C. The hammer pushes down on the nail, and the wood pushes up on the nail.
Incorrect. The two forces are both acting on the nail. In an action reaction pair, two objects act on each other.

D. The hammer pushes down on the wood, and the wood pushes up on the hammer.
Incorrect. The hammer and the wood do not directly act on each other.

A child is riding the merry-go-round when his shoe falls off. What will the path of the shoe be as it falls to the ground?

A. The shoe will continue to curve in the direction that the child is turning because Newton’s first law states that objects tend to maintain their original motion.
Incorrect. Newton’s first law states that objects tend to maintain straight-line motion in the absence of outside forces.

B. The shoe will curve away from the child because of the centrifugal forces on it.
Incorrect. Newton’s first law states that objects tend to maintain straight-line motion in the absence of outside forces.

C. The shoe will stop and fall straight to the ground because the child’s foot is no longer pushing it.
Incorrect. Newton’s first law states that objects tend to maintain straight-line motion in the absence of outside forces.

D. The shoe will continue in a straight line because Newton’s first law states that objects tend to maintain straight-line motion.
Correct! Newton’s first law states that objects tend to maintain straight-line motion in the absence of outside forces.

How long will it take an object to fall 30 meters from rest in the absence of air resistance?

A. 2.5 seconds
Correct! A fall of 30 meters would take approximately 2.5 seconds.

B. 3.1 seconds B. 3.1 seconds
Incorrect. You solved using a constant velocity of 9.8 m/s, you need to use a constant acceleration of 9.8 m/s2.

C. 24.2 seconds
Incorrect. 24.2 is the value of the velocity at the end of the fall. The question asked for the time of fall.

D. 6.1 seconds
Incorrect. You need to finish the calculation by taking the square root of 6.1.

Car A is traveling at a constant velocity of 15 m/s when it passes car B that is initially at rest. At the moment that car A passes, car B begins to accelerate at 3 m/s2. How far will the two cars travel before car B catches car A?

A. 10 meters
Incorrect. The cars meet after 10 seconds, not 10 meters.

B. 75 meters
Incorrect. At 75 meters, car B will have the same velocity as car A, not the same position.

C. 150 meters
Correct! The cars meet after they travel 150 meters.

D. 45 meters
Incorrect. Set the displacements of the two cars equal to one another and solve for time. Then use the time to solve for displacement.

A student throws a ball horizontally at 10 m/s from the top of a 60-meter-tall cliff. How far from the base of the cliff will the ball land? (Ignore air resistance.)

A. 3.5 meters
Incorrect. The ball will be in the air for 3.5 seconds, now solve for horizontal distance.

B. 6 meters
Incorrect. The 10 m/s is a horizontal velocity, and the 60 meters is a vertical distance. The two must be kept separate.

C. 60 meters
Incorrect. 60 meters is the height of the cliff, not the horizontal displacement.

D. 35 meters
Correct! The ball will travel 35 meters from the cliff before hitting the ground.

Maria throws two toys from the balcony of her apartment at the same time. Toy A has an initial velocity of +10 m/s, while toy B has an initial velocity of -10 m/s. Which of the following statements is true?

A. Toy B will hit the ground first going faster than toy A.
Incorrect. The toys had the same initial speed, displacement, and acceleration. They will have the same final speed.

B. Toy B will hit the ground first going slower than toy A.
Incorrect. The toys had the same initial speed, displacement, and acceleration. They will have the same final speed.

C. Toy B will hit the ground first at the same speed as toy A.
Correct! The toys had the same initial speed, displacement, and acceleration. They will have the same final speed.

D. The toys will hit the ground at the same time at the same speed.
Incorrect. Since toy B was thrown down at the same time, it will hit the ground before toy A.

An object that is moving along the x-axis with a negative velocity and positive acceleration is —

A. moving to the right and speeding up
Incorrect. A negative velocity indicates motion to the left; and since the velocity and acceleration have opposite signs, the object is slowing down.

B. moving to the right and slowing down
Incorrect. The negative velocity indicates motion to the left.

C. moving to the left and speeding up
Incorrect. Since the velocity and acceleration have opposite signs, the object is slowing down.

D. moving to the left and slowing down
Correct! A negative velocity indicates motion to the left; and since the velocity and acceleration have opposite signs, the object is slowing down.

A 75 kg person is standing on a scale in an elevator. What will the scale read if the elevator is moving up with a velocity of 4 m/s and slowing with an acceleration of -2 m/s2?

A. 735 N
Incorrect. This is the person’s weight. It is what the scale would read if the elevator were at rest or moving with a constant velocity.

B. 585 N
Correct! Since the acceleration is -2, the reading of the scale is reduced by 150 Newtons (2 × 75).

C. 885 N
Incorrect. The reading of the scale should have been reduced by 150 Newtons, not increased.

D. 1035 N
Incorrect. The reading of the scale is affected by the acceleration, not the velocity.

The velocity of a 5 kg object is shown on the following graph. What is the magnitude of the net force acting on the object?

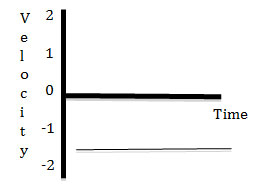
Velocity vs. time graph with a horizontal line at -2.

A. 10 N
Incorrect. The acceleration is 0, so the force is also 0.

B. -10 N
Incorrect. The acceleration is 0, so the force is also 0.

C. -2 N
Incorrect. The value of the velocity is -2, not the force.

D. 0 N
Correct! The acceleration is 0, so the force is also 0.

A student is using a ticker-tape timer to analyze the motion of an object. The tape the student used is shown below.

Ticker tape with equally spaced dots

Which of the following statements best describes the motion of the object?

A. The object was speeding up.
Incorrect. If the object were speeding up, the dots would be getting farther apart.

B. The object was slowing down.
Incorrect. If the object were slowing down, the dots would be getting closer together.

C. The object was moving at a constant velocity.
Correct! The dots are equally spaced.

D. The object was stationary.
Incorrect. If the object were stationary, there would only be one dot.

A sprinter accelerates uniformly from rest to a velocity of 7 m/s over a displacement of 10 meters. What was his average acceleration?

A. 2.45 m/s2
Correct! The time independent equation is the correct one to use.

B. 0 m/s2
Incorrect. Zero is the value of the initial velocity.

C. 2.9 m/s2
Incorrect. 2.9 is the value of the time it takes to cover 10 meters.

D. 7 m/s2
Incorrect. 7 is the value of the final velocity.

Two cars that are initially separated by 200 meters are moving toward one another. The first car is moving to the right at 10 m/s. The second car is moving to the left at 15 m/s.Where will the two cars meet? (Give your answer relative to the initial position of the first car.)

A. 8 meters from the initial position of the first car
Incorrect. Eight is the value of the time in seconds that it will take for the cars to meet.

B. 80 meters from the initial position of the first car
Correct! After eight seconds, they will meet 80 meters from the initial position of the first car.

C. 120 meters from the initial position of the first car
Incorrect. This is the position relative to the second car.

D. 40 meters from the initial position of the first car
Incorrect. If the cars were moving in the same direction, it would take 40 seconds for the faster car to catch the slower car.

Which of the following is true about the free body diagram drawn for an object being pulled to the right at a constant velocity across a rough floor?

A. The right-side arrow will be longer than the left-side arrow.
Incorrect. If the object is moving at a constant velocity, the forces balance.

B. The left-side arrow will be longer than the right-side arrow.
Incorrect. If the object is moving at a constant velocity, the forces balance.

C. The left-side and right-side arrows will be the same size.
Correct! If the object is moving at a constant velocity, the forces balance.

D. There are no arrows on the right or left sides of the diagram.
Incorrect. There are forces to the right and left, and arrows must represent them.

A space ship is flying horizontally over the surface of the moon when a package is dropped from the cargo hold. Where will the package land relative to the ship?

A. The package will land in front of the ship.
Incorrect. The package will have the same horizontal velocity as the ship.

B. The package will land behind the ship.
Incorrect. The package will have the same horizontal velocity as the ship.

C. The package will land directly below the ship.
Correct! The package will have the same horizontal velocity as the ship.

D. The package will not fall because there is no gravity in space.
Incorrect. There is gravity near the surface of the moon.

A child runs as fast as she can horizontally from the 10-meter diving platform. If she lands in the water 4.3 meters from the bottom of the platform, how fast was she running?

A. 3 m/s
Correct! It takes about 1.43 seconds to fall 10 meters, so her velocity must have been 3 m/2.

B. 1.43 m/s
Incorrect. It would take her about 1.43 seconds to fall 10 meters.

C. 14 m/s
Incorrect. This would be her vertical velocity just before hitting the water.

D. 0 m/s
Incorrect. This would be her vertical velocity just after leaving the platform.

If an object in constant circular motion at a velocity of 4 m/s feels a centripetal acceleration of 2 m/s2, what is the radius of its path?

A. 0.707 m
Incorrect. You solved square root of the result of acceleration divided by velocity. You need velocity squared divided by acceleration.

B. 1.414 m
Incorrect. You solved square root of the result of velocity divided by acceleration. You need velocity squared divided by acceleration.

C. 1.000 m
Incorrect. You solved velocity divided by acceleration squared. You need velocity squared divided by acceleration.

D. 8.000 m
Correct! This is velocity squared divided by acceleration.

A student taking data in an investigation of the motion of a fan cart noticed that the cart moved 1 cm during the first second, 3 cm during the second, 5 cm during the third second, and 7 cm during the fourth second. Which of the following best describes the motion of the fan cart?

A. The cart is moving with a constant velocity.
Incorrect. If the velocity were constant, the displacement would be the same each second.

B. The cart is moving with a constant positive acceleration.
Correct! The displacement for each second is increasing.

C. The cart is moving with a constant negative acceleration.
Incorrect. If the acceleration were negative, the displacement would be decreasing.

D. The cart is moving with a constantly increasing acceleration.
Incorrect. The difference between consecutive displacements is staying the same, so the acceleration is constant.

A truck is moving at 20 m/s when the driver notices a cow crossing the road. After a 0.75-second reaction time, the driver slams on his brakes and slows at a constant rate of -4m/s2. What is the total stopping distance of the truck?

A. 15 meters
Incorrect. This is how far the truck moves during the reaction time.

B. 50 meters
Incorrect. This is how far the truck moves during the deceleration.

C. 65 meters
Correct! This is the total stopping distance.

D. 5.75 meters
Incorrect! This is the total time in seconds that it takes the truck to stop.

A group of students is given a challenge by their physics teacher to use a graph generated by a motion sensor to determine the acceleration of an object. Which of the following will determine the acceleration?

A. The slope of Velocity vs. Time
Correct! The slope of Velocity vs. Time is the acceleration.

B. The area under Velocity vs. Time
Incorrect. The area under Velocity vs. Time is the displacement.

C. The slope of Position vs. Time
Incorrect. The slope of Position vs. Time is the velocity.

D. The area under Position vs. Time
Incorrect. The area under Position vs. Time is not a physically meaningful quantity.

What physical quantity is represented by the slope of a Force vs. Acceleration graph?

A. Time
Incorrect. Newton’s second law tells you what the slope should be.

B. Mass
Correct! Newton’s second law tells you what the slope should be.

C. Velocity
Incorrect. Newton’s second law tells you what the slope should be.

D. Position
Incorrect. Newton’s second law tells you what the slope should be.

A car moves at 10 m/s for 5 seconds, 0 m/s for 3 seconds, and 5 m/s for 7 seconds. What was the average velocity of the car?

A. 5.0 m/s
Incorrect. That is the average of the velocities; you need to find the total displacement and the total time.

B. 5.7 m/s
Correct! You divided the total displacement by the total time.

C. 7.1 m/s
Incorrect. You need to divide by the total time, not just the time that the car is moving.

D. 15 m/s
Incorrect. This is the sum of the velocities; you need to find the total displacement and total time.

Consider the graph below describing the motion of an object. How would you use the graph to find the instantaneous velocity at a time t1?

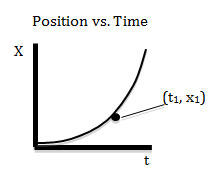
Parabolic Position vs. Time graph with point (t1, x1) labeled

A. Find the area under the curve from 0 to t1.
Incorrect. The area under a Position vs. Time graph is not the velocity.

B. Find the slope of a line tangent to the curve at t1.
Correct! The slope at one point is equal to the instantaneous velocity.

C. Find the slope between the two points (0,0) and (t1, x1).
Incorrect. This will give you an average velocity from t = 0 to t = t1.

D. Find the area under the curve at t1.
Incorrect. You cannot calculate the area under the curve at a single point.