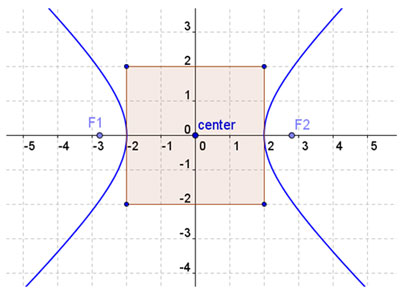
You may remember that for an ellipse, the foci are inside the closed curve of the ellipse. The hyperbola, however, is a pair of open curves that face outward from the center. The foci are within the curves, but outside the rectangle which is sketched to graph the hyperbola. Note: F1 and F2 in the figure below.

graph of hyperbola with foci at point (-2.8,0)and (2.8,0)

How do you find the location and coordinates of the foci of the hyperbola?

You must find the focal radius by using the following formula:

(major radius)2 + (minor radius)2 = (focal radius)2

In the figure above, both the major radius and the minor radius are 2 units, so:

22 + 22 = (focal radius)2 = 8 therefore, the = focal radius = √8 ˜ 2.8

This is the distance along the major axis (horizontal in this case) from the center to each focus.

So, what are the coordinates of the foci for the graph above?

Interactive popup. Assistance may be required.

Check Your Answer

(2.8, 0) and (-2.8, 0)Close Pop Up