As you will recall from your study of parent functions, adding a constant to a function shifts the function vertically. In this section, you will explore the effects of adding a constant to logarithmic and exponential functions.

Below are four functions, four graphs, and four descriptions of translations to the graphs of some exponential and logarithmic functions. Some functions, graphs, and descriptions have already been placed in the table. Place the remaining functions, graphs, and descriptions in the correct place.

Conclusion Questions

• What do you notice about the sign of the constant term in each function and the direction of the vertical translation?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The sign of the constant term tells you the direction of the vertical translation. If the sign is positive, then the vertical translation is upward. If the sign is negative, then the vertical translation is downward.

• What do you notice about the magnitude of the constant term in each function and the distance of the vertical translation?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The magnitude of the constant term tells you the distance of the vertical translation. For example, if the constant term is +7, then the vertical translation is 7 units upward. If the constant term is −3, then the vertical translation is 3 units downward.

Pause and Reflect

How does the vertical translation of exponential and logarithmic functions compare to the vertical translation of other functions, such as quadratic, square root, or rational functions?

Interactive popup. Assistance may be required.

Check Your Answer

The vertical translation of all functions works the same, regardless of the function family. The sign of the constant term tells you the direction of the vertical translation (upward or downward), and the number in the constant term tells you the distance of the translation.

Practice

1. Describe the vertical shift from the parent function for the function, r(x) = −6log(x – 9) – 3.

   Need a hint?

   Which parameter in the function controls the vertical shift or vertical translation of the graph of the function?

   Check Your Answer

   The vertical shift is 3 units down from the parent function.

2. If the graph of a function is shifted up 6 units from the parent function, which parameter has changed from the parent function?

   Need a hint?

   Which parameter in the function controls the vertical shift or vertical translation of the graph of the function?

   Check Your Answer

   A constant of 6 has been added to the parent function.

3. What has happened to the equation of k(x) = 10^x, to create the following graph:
   

   Need a hint?

   What would be the y-intercept of the parent function, k(x) = 10^x?

   Check Your Answer

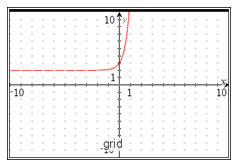
   A constant of 2 has been added.